图：最短路、最小生成树

最短路径

求解权重相同的最短路问题可以使用广度优先搜索方法。

• BFS（权重相同）、0-1 BFS

• Dijkstra（不能存在负权边）

一、单源最短路径问题

单源最短路径问题(single source shortest path，SSSP问题)

邻接矩阵表示

邻接表表示

https://leetcode.cn/problems/network-delay-time/solution/gong-shui-san-xie-yi-ti-wu-jie-wu-chong-oghpz/)

1. Dijkstra算法（无负权边）

邻接矩阵存储：

• 时间复杂度$O(n^2+m)$，求未访问的距离最近节点O(n)，总共n个节点，m条边

• 空间复杂度：$O(n^2)$

邻接表存储：

• 时间复杂度：$O(n^2+m)$

• 空间复杂度：$O(n+m)$

堆优化：（采用邻接表存储，堆优化是寻找最近未被访问节点）

• 时间复杂度：$O(mlogm)$

• 空间复杂度：$O(n+m)$

稠密图(边数远大于点数)，运行时间上，枚举写法要略快于堆的写法。

a. 邻接矩阵存储

/*
	edge=[from, to, weight] 表示图中的边连接和权重
*/
Dijkstra(vector<vector<int>> edges,int n,int src){
    //根据边建图，用邻接矩阵表示，区分有向图和无向图
    vector<vector<int>> graph(n,vector<int>(n, -1));
    for(auto &edge:edges){
        int from=edge[0],to=edge[1],weight=edge[2];
        graph[from][to]=weight;
    }
    
    //dist[i]表示从src到i的最短距离
    vector<int> dist(n, INT_MAX);
    //记录点i是否被访问过
    vector<bool> visited(n,false); 
    
    //初始化src点
    dist[src]=0;
    
    //需要求到其余n-1个点的距离
  	for(int i=0;i<n;i++){
        //寻找未访问的最近的结点
        int u=-1;
        for(int j=0;j<n;j++){
            if(!visited[j]&&(u==-1||dist[j]<dist[u]))
                u=j;
        }
        //存在节点不可达的情况
        if(dist[u]==INT_MAX){
            break;
        }
        visited[u]=true;
        //遍历u结点的临边
        //可以将不存在的边初始化为一个较大的值，这样在这里不需要判断是否存在边
        for(int k=0;k<n;k++){
            if(graph[u][k]!=-1)
                dist[k]=min(dist[k],dist[u]+graph[u][k]);
        }
    }
}

b. 邻接表存储

/*
	edge=[from, to, weight] 表示图中的边连接和权重
*/
Dijkstra(vector<vector<int>> edges,int n,int src){
    //根据边建图，用邻接矩阵表示，区分有向图和无向图
    vector<vector<pair<int,int>>> graph(n);
    for(auto &edge:edges){
        int from=edge[0],to=edge[1],weight=edge[2];
        g[from].push_back({to,weight});
    }
    
    //dist[i]表示从src到i的最短距离
    vector<int> dist(n, INT_MAX);
    //记录点i是否被访问过
    vector<bool> visited(n,false); 
    
    //初始化src点
    dist[src]=0;
    
    //需要求到其余n-1个点的距离
  	for(int i=0;i<n;i++){
        //寻找未访问的最近的结点
        int u=-1;
        for(int j=0;j<n;j++){
            if(!visited[j]&&(u==-1||dist[j]<dist[u]))
                u=j;
        }
        //存在节点不可达的情况
        if(dist[u]==INT_MAX){
            break;
        }
        visited[u]=true;
        //遍历u结点的临边
        for(auto &[v,w]:graph[u]){
            dis[v]=min(dis[v],dis[u]+w);
        }
    }
}

c. 堆优化的Dijkstra算法

/*
	edge=[from, to, weight] 表示图中的边连接和权重
*/
typedef pair<int,int> pii;
Dijkstra(vector<vector<int>> edges,int n,int src){
    //根据边建图，用邻接矩阵表示，区分有向图和无向图
    vector<vector<pair<int,int>>> graph(n);
    for(auto &edge:edges){
        int from=edge[0],to=edge[1],weight=edge[2];
        g[from].push_back({to,weight});
    }
    
    //dist[i]表示从src到i的最短距离
    vector<int> dist(n, INT_MAX);
    
    //初始化src点
    dist[src]=0;
    
	priority_queue<pii,vector<pii>,greater<>> pq;
    pq.push({0,src});
    
   	while(!pq.empty()){
        auto [cost,u]=pq.top();
        pq.pop();
        // 下图红色部分给出了说明
        if(dis[u]<cost){
            continue;
        }
        
        for(auto &[v,w]:g[u]){
            int d=dis[u]+w;
            if(d<dis[v]){
                dis[v]=d;
                pq.push({d,v});
            }
        }
    }
}

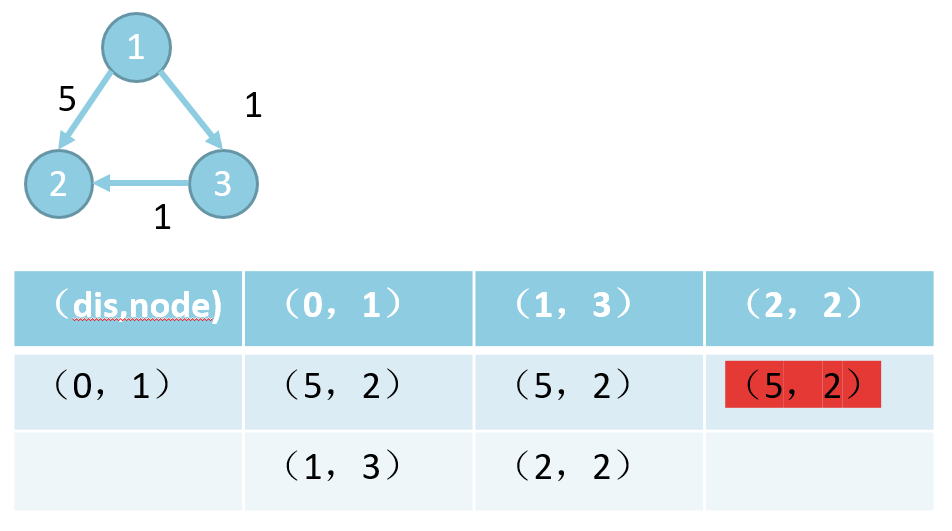
2. 0-1 BFS

class Solution {
  public:
    const int inf = INT_MAX / 2;
    vector<vector<int>> direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    int minCost(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dis(m, vector<int>(n, inf));
        vector<vector<bool>> vis(m, vector<bool>(n, false));
        deque<int> dq;

        dis[0][0] = 0;
        dq.push_back(0);
        while (!dq.empty()) {
            int node = dq.front();
            dq.pop_front();

            int x = node / n, y = node % n;
            if (vis[x][y]) {
                continue;
            }
            vis[x][y] = true;
            for (int k = 0; k < 4; k++) {
                int p = x + direction[k][0], q = y + direction[k][1];
                if (p >= 0 && p < m && q >= 0 && q < n) {
                    int newD = dis[x][y] + (k + 1 != grid[x][y]);
                    if (newD < dis[p][q]) {
                        dis[p][q] = newD;
                        if (grid[x][y] == k + 1) {
                            dq.push_front(p * n + q);
                        } else {
                            dq.push_back(p * n + q);
                        }
                    }
                }
            }
        }
        return dis[m - 1][n - 1];
    }
};

3. Bellman Ford（负权图中求最短边）

SPFA算法（shortest path fastest algorithm）

二、任意两点之间的最短路径

Flyod算法
$$
\begin{align}
&dp[0][i][j]：初始边权重\
&dp[k+1][i][j]：表示从i到j经过的节点<=k的最短路径长度\
&不经过节点k：dp[k][i][j]\
&经过节点k：dp[k][i][k]+dp[k][k][j]
\end{align}

$$

class Solution {
  public:
    int findTheCity(int n, vector<vector<int>> &edges, int distanceThreshold) {
        vector<vector<vector<int>>> dp(n + 1,
                                       vector<vector<int>>(n, vector<int>(n)));
        vector<vector<int>> w(n,vector<int>(n,INT_MAX/2));
        for (auto &e : edges) {
            int u = e[0], v = e[1], wt = e[2];
            w[u][v]=w[v][u]=wt;
        }
        dp[0]=w;
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    dp[k + 1][i][j] =
                        min(dp[k][i][j], dp[k][i][k]+dp[k][k][j]);
                }
            }
        }

        int minCnt = INT_MAX;
        int node = -1;
        for (int i = 0; i < n; i++) {
            int cnt = 0;
            for (int j = 0; j < n; j++) {
                if (i != j && dp[n][i][j] <= distanceThreshold)
                    cnt++;
            }
            if (cnt <= minCnt) {
                minCnt = cnt;
                node = i;
            }
        }
        return node;
    }
};

空间优化
$$
\begin{align}
&dp[k+1][i][j]：表示从i到j经过的节点<=k的最短路径长度\
&不经过节点k：dp[k][i][j]（前一步计算的结果）\
&经过节点k：dp[k][i][k]+dp[k][k][j]\
&dp[k+1][i][k]=dp[k][i][k]（i到k，经过节点<=k，则中间节点肯定无k）\
&dp[k+1][k][j]=dp[k][k][j]
\end{align}

$$

class Solution {
  public:
    int findTheCity(int n, vector<vector<int>> &edges, int distanceThreshold) {
        vector<vector<int>> dp(n, vector<int>(n, INT_MAX / 2));
        for (auto &e : edges) {
            int u = e[0], v = e[1], wt = e[2];
            dp[u][v] = dp[v][u] = wt;
        }
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
                }
            }
        }

        int minCnt = INT_MAX;
        int node = -1;
        for (int i = 0; i < n; i++) {
            int cnt = 0;
            for (int j = 0; j < n; j++) {
                if (i != j && dp[i][j] <= distanceThreshold)
                    cnt++;
            }
            if (cnt <= minCnt) {
                minCnt = cnt;
                node = i;
            }
        }
        return node;
    }
};

Dijkstra和floyd区别

• Dijkstra不能处理负权图，Flyod能处理负权图；

• Dijkstra处理单源最短路径，Flyod是处理多源最短路径

• 在图确定后添加新的边，Flyod不用从头开始计算

题单

• 2642. 设计可以求最短路径的图类 - 力扣（LeetCode）（动态添加边适合Floyd）

• 743. 网络延迟时间

  • 【宫水三叶】涵盖所有的「存图方式」与「最短路算法（详尽注释）」 - 网络延迟时间 - 力扣（LeetCode）

• 882. 细分图中的可到达节点

• 1334. 阈值距离内邻居最少的城市

• 1368. 使网格图至少有一条有效路径的最小代价

• 1514. 概率最大的路径