位运算

发表于
统计数字二进制表示中含有的1的个数

从集合论到位运算，常见位运算技巧分类总结！ - 力扣（LeetCode）

位运算

常用的位运算符号包括：^按位异或，&按位与，|按位或，~取反，<<算术左移，>>算术右移

x^0=x x&0=0 x|0=x
x^1s=~x x&1s=x x|1s=1
x^x=0 x&x=x x|x=x
作用 操作 示例
去除n的二进制表示中最低的一位 n&(n-1) 11010&(11001)=11000
得到n的二进制表示中最低的一位 n&(-n) 11010&(00110)=00010
低位清0：[0:n]位清0 x & ~( (1<<(n+1)) -1 )
取反第n位 x^(1<<n)
c++位运算函数
n的二进制表示中有多少个1 __builtin_popcount(n)

异或

  • $x\oplus x=0$

  • $x\oplus 0=x$

  • $x\oplus y=y\oplus x$

  • $x\oplus y\oplus y=x$

  • $x\oplus y=z\Longrightarrow x\oplus z=y$

x x 结果
x&(-x)（得到最低位的1） x=16(10000) 10000
x&(x-1)（最低位1变为0） 17(10001) 10000

位运算基础知识

  1. 判断奇偶：

    • 奇：(x & 1) == 1  ⟺  if⟺(x & 1) != 0

    • 偶：(x & 1) == 0  ⟺  \iff⟺(x & 1) != 1

  2. 乘（或除）以 2 的幂次：

    • x >> n  ⟺  iff⟺x / 2^n

    • x << n  ⟺  \iff⟺x * 2^n

  3. 去除最后一位 1：x & (x - 1)

  4. 得到最后一位 1：x & -x

  5. 判断 2 的幂次：x & (x - 1) == 0

  6. 交换两个数：a ^= b; b ^= a; a ^= b;

  7. 交换符号：~x + 1  ⟺  \iff⟺-x

  8. 取绝对值：(x ^ x >> size(x) - 1) - (x >> size(x) - 1)  ⟺  \iff⟺x < 0 ? -x : x

  9. 构造 n 个 1：(1 << n) - 1

  10. 将最左边的 n 位清零：x & (~0 << n)

  11. 获取 x 的第 n 位值（0 或 1）：(x >> n) & 1

  12. 获取 x 的第 n 位的幂值：x & (1 << n)

  13. 仅将第 n 位置为 1：x | (1 << n)

  14. 仅将第 n 位置为 0：x & (~(1 << n))

  15. 将 x 最高位至第 n 位（含）清零：x & ((1 << n) - 1)

  16. 将第 n 位至第 0 位（含）清零：x & (~((1 << (n + 1)) - 1))

  17. 异或满足交换律、结合律：a ^ b ^ a = b ^ (a ^ a) = b ^ 0 = b面试题 05.01. 插入 - 力扣（LeetCode）

得到二进制数x最低位的1（lowbit）

x&-x

负数按照补码规则在计算机中存储，-n的二进制表示为n的二进制表示的每一位取反加1（包括符号位）

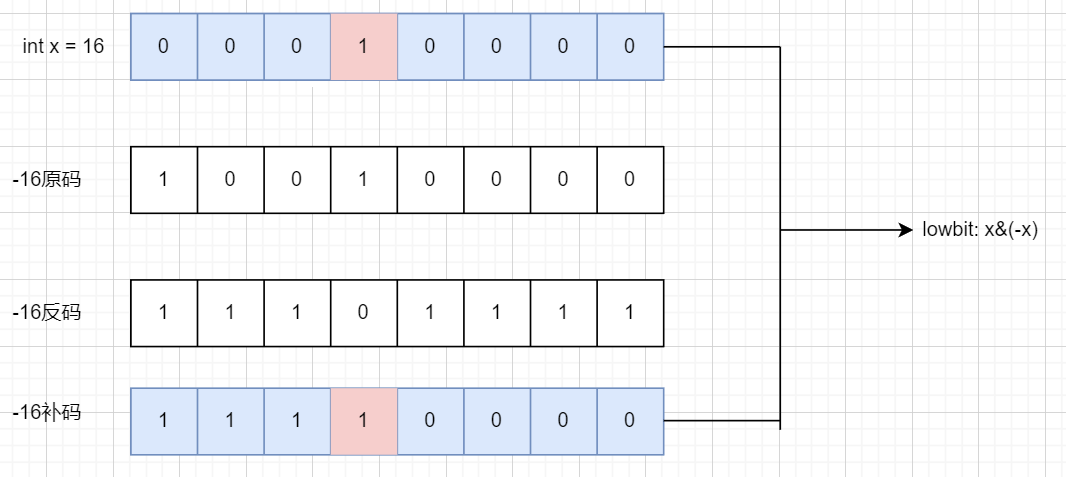
image-20221018105315154

二进制数最低位的1变成0

x=x&(x-1)

x-=(x&-x)

将二进制数x最低位的0变成1

x取反的最低位1是x的最低位0

y=~x

x|=y&(-y)

x=x| (x+1)

二进制特性

可以利用二进制和位运算输出一个数组的所有子集。假设有一个长度为n的数组，可以生成长度为n的所有二进制，1表示选取该数字，0表示不选取，可以得到$2^n$个子集。快速判断两个字符串是否含有重复字母：为每个字符串建立一个长度为26的二进制数字，每个位置表示是否存在该字母

位计数（统计1的数目）

cnt=0
while(x){
    x=x&(x-1);
    cnt++;
}

while(x){
    cnt+=x&1;
    x=x>>1;
}

__builtin_popcount(x)

Brian Kernighan算法

对于任意整数 xx，令 x=x & (x−1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则操作次数即为 x 的「一比特数」。

对于给定的 n，计算从 0 到 n 的每个整数的「一比特数」的时间都不会超过O(logn)，因此总时间复杂度为O(nlogn)。

c(x)表示二进制表示x中的1个数

c(x&y)+c(x|y)=c(x)+c(y)

image-20230510231250236

1318. 或运算的最小翻转次数

题目

异或

分享｜异或/XOR部分问题汇总 - 力扣（LeetCode）

题目 标签
421. 数组中两个数的最大异或值 - 力扣（LeetCode） 字典树
1720. 解码异或后的数组 - 力扣（LeetCode） 数学
1734. 解码异或后的排列 - 力扣（LeetCode） 数学
1863. 找出所有子集的异或总和再求和 - 力扣（LeetCode） 枚举子集（二进制状态枚举，递归枚举）
1310. 子数组异或查询 - 力扣（LeetCode） 异或前缀和
1829. 每个查询的最大异或值 - 力扣（LeetCode） 前缀异或和、异或最大值、技巧
268. 丢失的数字 - 力扣（LeetCode） 异或，非常巧妙，单一的数字变种题
$$ 
 \begin{align}
 &1734题\\
&(a,b,c,d,e)\\
&(x,y,z,w)\\
&\text{有5个数字}:y\oplus w=b\oplus c\oplus d\oplus e=p\\
&a\oplus b\oplus c\oplus d\oplus e=1\oplus 2\oplus 3\oplus 4\oplus 5=q\\
&a=q\oplus(b\oplus c\oplus d\oplus e)=q\oplus p
&\end{align}
$$