动态规划

发表于 2023-02-28 分类于算法

一维DP、二维DP、空间压缩、背包DP、区间DP、数位DP。适合求解具有最优子结构的问题，并且子问题的最值可以得到。

def comb(a,b):
    if a*b==0:
        return a+b
    elif a%10==b%10:
        return comb(a//10,b//10)*10+a%10
    return min(comb(a//10,b)*10+a%10,comb(a,b//10)*10+b%10)

1 动态规划DP

边界条件+转移方程

DP - OI Wiki (oi-wiki.org)

2 空间压缩

2.1 只与有限个变量相关

2.1.1.1 91. 解码方法

class Solution {
public:
    int numDecodings(string s) {
        int n=s.size();
        vector<int> dp(n+1);
        dp[0]=1;

        for(int i=0;i<n;i++){
            // 当前位置不为0，可选择一个数字映射到字母
            if(s[i]!='0')
                dp[i+1]=dp[i];
            
            // 选两个位置数字映射
            if(i>0){
                int val=(s[i-1]-'0')*10+s[i]-'0';
                if(val<=26&&val>=10)
                    dp[i+1]+=dp[i-1];
            }
        }
        return dp[n];
    }
};

空间优化

class Solution {
public:
    int numDecodings(string s) {
        int n=s.size();
        int a=0,b=1,c;
        for(int i=0;i<n;i++){
            c=0;
            // 当前位置不为0，可选择一个数字映射到字母
            if(s[i]!='0')
                c=b;;
            
            // 选两个位置数字映射
            if(i>0){
                int val=(s[i-1]-'0')*10+s[i]-'0';
                if(val<=26&&val>=10)
                    c+=a;;
            }
            tie(a,b)={b,c};
        }
        return c;
    }
};

2.2 二维压缩到一维

2.2.1.1 64. 最小路径和

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size(),n=grid[0].size();
        vector<vector<int>> dp(m,vector<int>(n));
        dp[0][0]=grid[0][0];

        for(int i=1;i<n;i++)
            dp[0][i]=dp[0][i-1]+grid[0][i];
        for(int i=1;i<m;i++)
            dp[i][0]=dp[i-1][0]+grid[i][0];

        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++)
                dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
        }
        return dp[m-1][n-1];
    }
};

dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]只与两个数有关，可以压缩到一维。对于第i行，在求第j列时，前j-1列已经更新，dp[j-1]代表dp[i][j-1]；dp[j]待更新，当前存储dp[i-1][j]。

class Solution {
  public:
    int minPathSum(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> dp(n);
        dp[0]=grid[0][0];
        for (int j = 1; j < n; j++)
            dp[j]=dp[j-1]+grid[0][j];
        for (int i = 1; i < m; i++) {
            dp[0]+=grid[i][0];
            for(int j=1;j<n;j++)
                dp[j]=min(dp[j],dp[j-1])+grid[i][j];
        }
        return dp[n-1];
    }
};

2.3 滚动数组

2.3.1.1 221. 最大正方形

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size(),n=matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        int ret=0;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(matrix[i-1][j-1]=='1'){
                    int edge=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]));
                    dp[i][j]=edge+1;
                    ret=max(ret,edge+1);
                }
            }
        }
        return ret*ret;
    }
};

滚动数组压缩，只需要保存两行的结果。在位置为0时需要修改相应值，否则记录的是前面两行对应列位置的值。

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size(),n=matrix[0].size();
        vector<vector<int>> dp(2,vector<int>(n+1));
        int ret=0;
        for(int i=1;i<=m;i++){
            int idx=i%2;
            for(int j=1;j<=n;j++){
                if(matrix[i-1][j-1]=='1'){
                    int edge=min(dp[1-idx][j-1],min(dp[1-idx][j],dp[idx][j-1]));
                    dp[idx][j]=edge+1;
                    ret=max(ret,edge+1);
                }
                //关键
                else{
                    dp[idx][j]=0;
                }
            }
        }
        return ret*ret;
    }
};

3 二维DP

72. 编辑距离（583题的动态规划的变体）

给你两个单词 word1 和 word2，请返回将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符、删除一个字符、替换一个字符

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m=word1.size(),n=word2.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        for(int i=1;i<=m;i++)
            dp[i][0]=i;
        for(int j=1;j<=n;j++)
            dp[0][j]=j;

        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(word1[i-1]==word2[j-1])
                    dp[i][j]=dp[i-1][j-1];
                else
                    // word1删除一个字符 word2删除一个字符 替换一个字符
                    dp[i][j]=min( min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;
            }
        }

        return dp[m][n];
    }
};

4 背包DP

背包问题是一种组合优化的 NP 完全问题：有 N 个物品和容量为 W 的背包，每个物品都有自己的体积 w 和价值 v，求拿哪些物品可以使得背包所装下物品的总价值最大。如果限定每种物品只能选择 0 个或 1 个，则问题称为 0-1 背包问题；如果不限定每种物品的数量，则问题称为无界背包问题或完全背包问题。

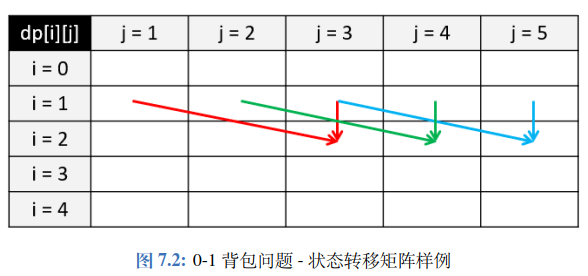
4.1 0-1背包

$$
前i件物品体积不超过j的情况下能达到的最大价值\
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w_i])+v_i\
时间复杂度：O(NM)\
空间复杂度：O(NM)
$$

//N个物品，体积最大为W
int maxValue(vector<int> weights,vector<int> values,int N,int W){
 	vector<vector<int>> dp(N+1,vector<int>(W+1,0));
    for(int i=1;i<=N;i++){
        int w=weights[i-1],v=values[i-1];
        for(int j=1;j<=W;j++){
            if(j>=w){
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-w]+v);
            }else{
                dp[i][j]=dp[i-1][j];
            }
        }
    }
    return dp[N][W];
}

空间优化：

int maxValue(vector<int> weights,vector<int> values,int N,int W){
 	vector<vector<int>> dp(N+1,vector<int>(W+1,0));
    vector<int> dp(W+1,0);
    for(int i=1;i<=N;i++){
        int w=weights[i-1],v=values[i-1];
        for(int j=W;j>=w;j--){
           dp[j]=max(dp[j],dp[j-w]+v);
        }
    }
    return dp[W];
}

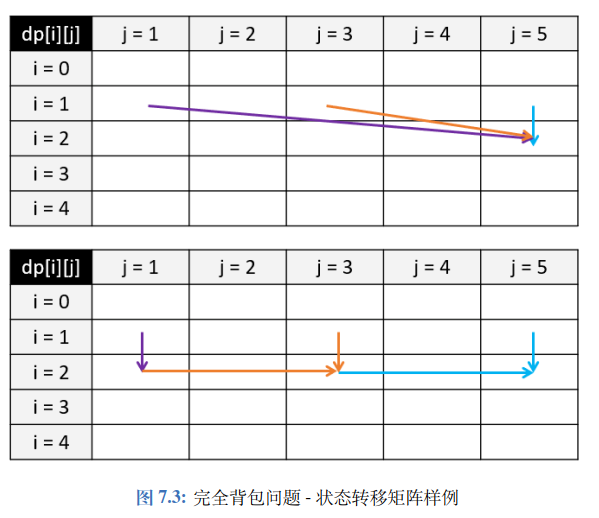
4.2 完全背包

假设物品$i=2,w=2,v=3$，
$$
\begin{aligned}
dp[2][5]=max(dp[1][5],dp[1][3]+3,dp[1][1]+6)\
dp[2][3]=max(dp[1][3],dp[1][1]+3)\
\Longrightarrow dp[2][5]=max(dp[1][5],dp[2][3]+3)\
完全背包：dp[i][j]=max(dp[i-1][j],dp[i][j-w]+v)\
0-1背包：dp[i][j]=max(dp[i-1][j],dp[i-1][j-w]+v)
\end{aligned}
$$

//N个物品，体积最大为W
int maxValue(vector<int> weights,vector<int> values,int N,int W){
 	vector<vector<int>> dp(N+1,vector<int>(W+1,0));
    for(int i=1;i<=N;i++){
        int w=weights[i-1],v=values[i-1];
        for(int j=1;j<=W;j++){
            if(j>=w){
                dp[i][j]=max(dp[i-1][j],dp[i][j-w]+v);
            }else{
                dp[i][j]=dp[i-1][j];
            }
        }
    }
    return dp[N][W];
}

//空间优化
//N个物品，体积最大为W
int maxValue(vector<int> weights,vector<int> values,int N,int W){
 	vector<int> dp(W+1,0);
    for(int i=1;i<=N;i++){
        int weight=weights[i-1],v=values[i-1];
        for(int j=weight;j<=W;j++){
           dp[j]=max(dp[j],dp[j-weight]+v);
        }
    }
    return dp[W];
}

4.2.1.1 474. 一和零

$$
dp[i][j][k]=max(dp[i-1][j][k],dp[i-1][j-zero][k-one])
$$

从三维压缩到二维，因此需要倒序遍历

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));

        for(string &s:strs){
            int zero=0,one=0;
            for(char ch:s){
                if(ch=='1')
                    one++;
                else
                    zero++;
            }
            for(int i=m;i>=zero;i--){
                for(int j=n;j>=one;j--){
                   dp[i][j]=max(dp[i][j],dp[i-zero][j-one]+1);
                }
            }
        }
        return dp[m][n];
    }
};

2902. 和带限制的子多重集合的数目 - 力扣（LeetCode）

0-1背包：

416. 分割等和子集
474. 一和零
494. 目标和（回溯，DP）
$$
选取部分数字构成负数：\
(sum-neg)-neg=target\
neg=\frac{sum-target}{2}\
\
选取部分数字构成正数：\
act-neg=target\
act+neg=sum\
act=\frac{sum+target}{2}
$$
[ ]
879. 盈利计划
1049. 最后一块石头的重量 II

完全背包：

322. 零钱兑换

目标和 - 目标和 - 力扣（LeetCode）

5 字符串编辑

5.1.1.1 10. 正则表达式匹配

class Solution {
  public:
    bool isMatch(string s, string p) {
        int m = s.size(), n = p.size();
        vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
        dp[0][0] = true;

        for (int i = 1; i <= n; i++) {
            if (p[i - 1] == '*')
                dp[0][i] = dp[0][i - 2];
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p[j - 1] == '.') {
                    dp[i][j] = dp[i - 1][j - 1];
                } else if (p[j - 1] != '*') {
                    dp[i][j] = dp[i - 1][j - 1] && (s[i - 1] == p[j - 1]);
                } else if (p[j - 2] != '.' && p[j - 2] != s[i - 1]) {
                    // 不用前面那个字符
                    dp[i][j] = dp[i][j - 2];
                } else {
                    // 用0次，再用一次，用一次(用一次的情况会被遍历到)
                    dp[i][j] = dp[i][j - 2] || dp[i - 1][j] ;//|| dp[i][j - 1];
                }
            }
        }
        return dp[m][n];
    }
};

1143. 最长公共子序列

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m=text1.size(),n=text2.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));

        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(text1[i-1]==text2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[m][n];
    }
};

#### 522. 最长特殊序列 II

双指针判断s1是否是s2的子序列

class Solution {
public:
    int findLUSlength(vector<string>& strs) {
        auto is_subseq = [](const string& s, const string& t) -> bool {
            int pt_s = 0, pt_t = 0;
            while (pt_s < s.size() && pt_t < t.size()) {
                if (s[pt_s] == t[pt_t]) {
                    ++pt_s;
                }
                ++pt_t;
            }
            return pt_s == s.size();
        };

        int n = strs.size();
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            bool check = true;
            for (int j = 0; j < n; ++j) {
                if (i != j && is_subseq(strs[i], strs[j])) {
                    check = false;
                    break;
                }
            }
            if (check) {
                ans = max(ans, static_cast<int>(strs[i].size()));
            }
        }
        return ans;
    }
};

72. 编辑距离

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m=word1.size(),n=word2.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX/2));
        dp[0][0]=0;
        for(int j=1;j<=n;j++) dp[0][j]=j;
        for(int i=1;i<=m;i++) dp[i][0]=i;

        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(word1[i-1]==word2[j-1]){
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    // 对word1插入一个字符，与word2[j]匹配
                    // 对word1删除一个字符，word1[i-1]与word2[j]匹配
                    // 替换一个字符
                    dp[i][j]=min(dp[i][j-1],min(dp[i-1][j],dp[i-1][j-1]))+1;
                }
            }
        }
        return dp[m][n];
    }
};

空间优化

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m=word1.size(),n=word2.size();
        vector<vector<int>> dp(2,vector<int>(n+1,INT_MAX/2));
        for(int j=0;j<=n;j++) dp[0][j]=j;

        for(int i=1;i<=m;i++){
            int idx=i%2;
            dp[idx][0]=i;
            for(int j=1;j<=n;j++){
                if(word1[i-1]==word2[j-1]){
                    dp[idx][j]=dp[1-idx][j-1];
                }else{
                    // 对word1插入一个字符，与word2[j]匹配
                    // 对word1删除一个字符，word1[i-1]与word2[j]匹配
                    // 替换一个字符
                    dp[idx][j]=min(dp[idx][j-1],min(dp[1-idx][j],dp[1-idx][j-1]))+1;
                }
            }
        }
        return dp[m%2][n];
    }
};

650. 只有两个键的键盘（同过乘除计算位置）
[ ]

6 区间DP

6.1 定义

区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。

令状态$f(i,j)$表示将下标位置$i$到$j$的所有元素合并能获得的价值的最大值，那么 $f(i,j)=\max{f(i,k)+f(k+1,j)+cost}$为将这两组元素合并起来的代价。

6.2 性质

区间 DP 有以下特点：

合并：即将两个或多个部分进行整合，当然也可以反过来；

特征：能将问题分解为能两两合并的形式；

求解：对整个问题设最优值，枚举合并点，将问题分解为左右两个部分，最后合并两个部分的最优值得到原问题的最优值。

7 数位DP

/**
 s:对上边界数字转为字符串
 i:当前填第i个数字
 mask: 标记已经填过了哪些数字（数字不可重复使用）
 isLimited：当前位置填入数字是否受到限制
 isNum：前面是否填过数字（数字是否可以从0开始）
 dp：记忆化搜索，记录已经查找过的结果，dp[i][j]表示前面[:i-1]的情况为j，第i位数字及其之后共有多少种选择
*/
//backtrack(s,i,mask,isLimited,isNum,dp)从左到右填第i位及其之后数位的合法方案数
int backtrack(s,i,mask,isLimited,isNum,dp){
    if(i==s.size())
        return isNum;
   	if(!isLimited&&isNum&&dp[i][mask]>=0)
        return dp[i][mask]
    int res=0;
    if(!isNum)
        res+=backtrack(s,i+1,mask,false,false,dp);
   	
    int up=isLimited?s[i]-'0':9;
    //前面已经填过数字，当前位置可以填0，否则填1
    for(int d=1-isNum;d<=up;d++){
        //数字d未使用过
        if((mask&(1<<d))==0){
            res+=backtrack(s,i+1,mask|1<<d,isLimited&&d==up,true,dp);
        }       
    }
    //缓存当前结果
    if(!isLimited&&isNum)
        dp[i][mask]=res;
   	return res;
}

7.1.1 题目

7.1.1.1 6957. 统计范围内的步进数字数目

取模相减结果为负数

class Solution {
public:
    const int MOD=1e9+7;
    int countSteppingNumbers(string low, string high) {
        int m=low.size(),n=high.size();
        vector<vector<int>> dp1(n,vector<int>(10,-1)),dp2(m,vector<int>(10,-1));

        int r=backtrack(high,0,false,true,dp1,-1);
        int l=backtrack(low,0,false,true,dp2,-1);

        return ((r-l)+MOD+valid(low))%MOD;
    }

    bool valid(string s){
        int n=s.size();
        for(int i=1;i<n;i++){
            if(abs(s[i]-s[i-1])!=1)
                return false;
        }
        return true;
    }

    int backtrack(string &s,int i,bool isNum,bool isLimit,vector<vector<int>>& dp,int pre){
        if(i==s.size())
            return isNum;
        
        if(!isLimit&&isNum&&dp[i][pre]!=-1)
            return dp[i][pre];
        
        long long res=0;
        if(!isNum)
            res+=backtrack(s,i+1,false,false,dp,-1);
        
        int up=isLimit?s[i]-'0':9;
        for(int d=1-isNum;d<=up;d++){
            if(pre==-1||abs(d-pre)==1)
                res=(res+backtrack(s,i+1,true,isLimit&&d==up,dp,d))%MOD;
        }
        
        if(isNum&&!isLimit)
            dp[i][pre]=res;
        return res;
    }
};

7.1.1.2 2719. 统计整数数目

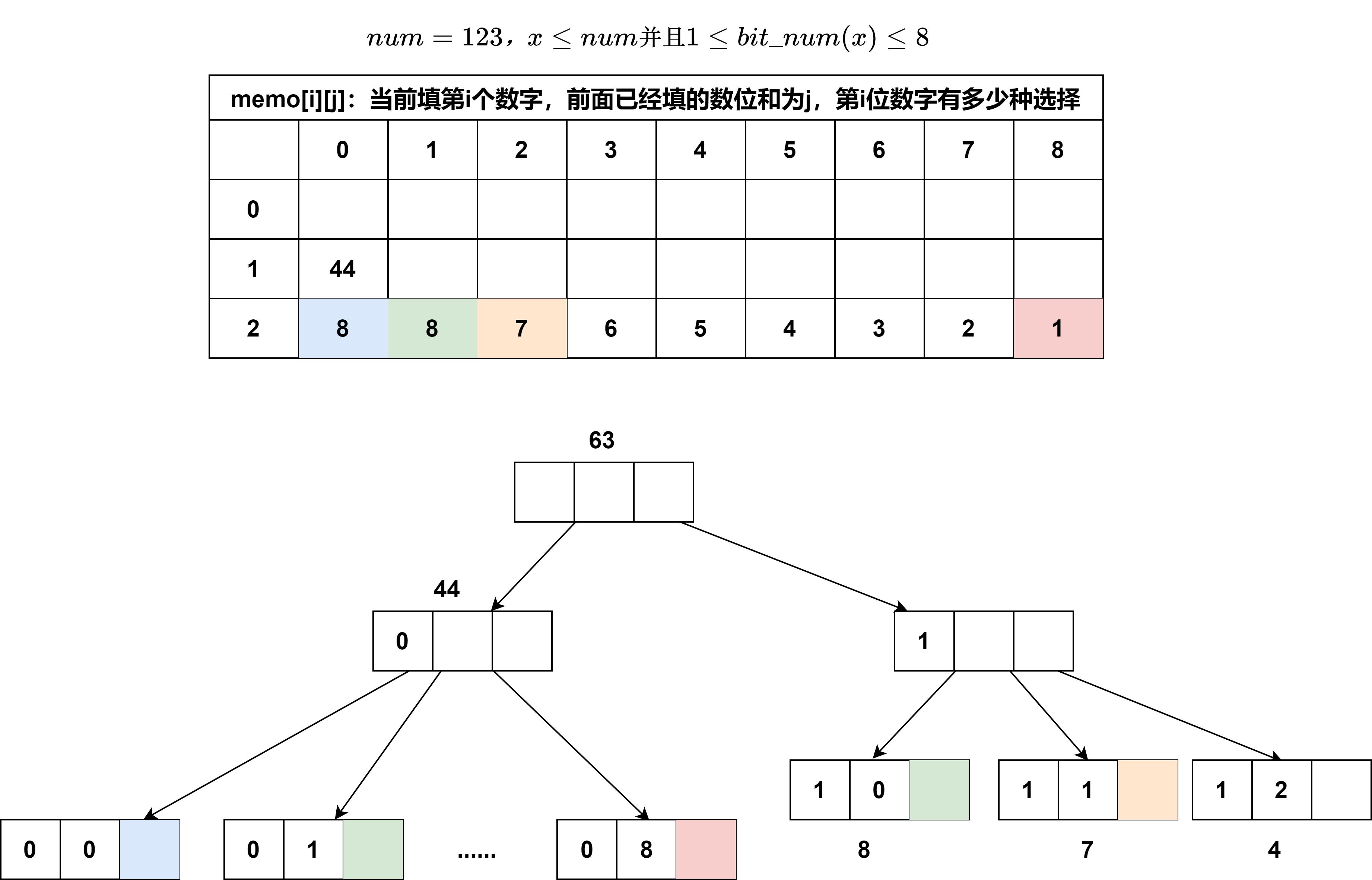
class Solution1 {
  public:
    const int MOD = 1e9 + 7;
    int count(string num1, string num2, int min_sum, int max_sum) {
        int ans = (helper(num2, min_sum, max_sum) + MOD -
                   helper(num1, min_sum, max_sum)) %
                  MOD;
        int sum = 0;
        for (char &ch : num1) {
            sum += ch - '0';
        }
        ans += sum >= min_sum && sum <= max_sum;
        return ans;
    }
    // 计算x<=num，且min_sum<=x<=max_sum数字个数
    int helper(string &num, int &min_sum, int &max_sum) {
        int n = num.size();
        // 编译器不支持变长数组声明
        // int memo[n][min(9 * n, max_sum) + 1];
        // memset(memo, -1, sizeof(memo));
        vector<vector<int>> memo(n, vector<int>(min(9 * n, max_sum) + 1, -1));
        function<int(int, int, bool)> f = [&](int i, int sum,
                                              bool isLimited) -> int {
            if (sum > max_sum) {
                return 0;
            }
            if (i == num.size()) {
                return sum >= min_sum;
            }

            if (!isLimited && memo[i][sum] != -1) {
                return memo[i][sum];
            }
            int res = 0;
            int up = isLimited ? num[i] - '0' : 9;
            for (int d = 0; d <= up; d++) {
                res = (res + f(i + 1, sum + d, isLimited && d == up)) % MOD;
            }
            if (!isLimited)
                memo[i][sum] = res;
            return res;
        };
        int res = f(0, 0, true);
        return res;
    }
};

7.1.1.3 600. 不含连续1的非负整数

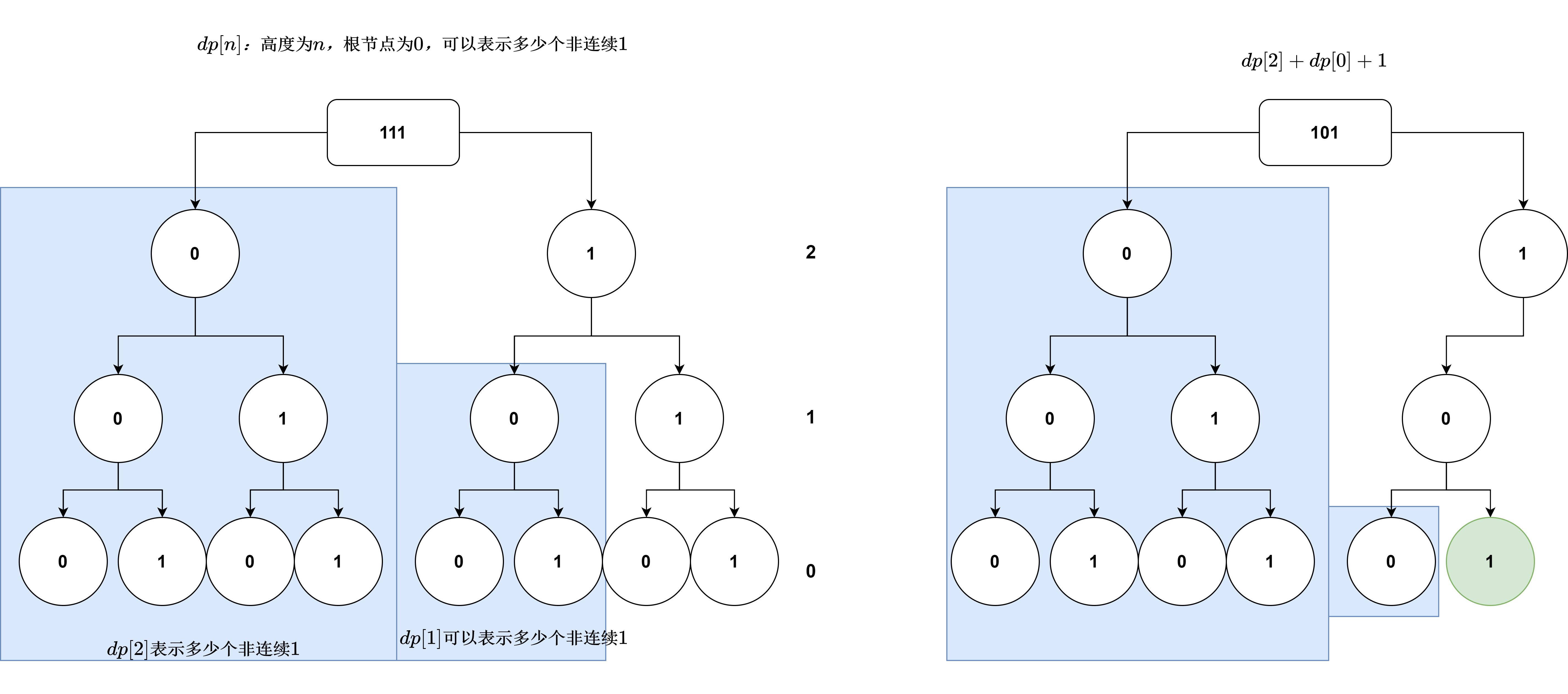
给定一个正整数 n ，请你统计在 [0, n] 范围的非负整数中，有多少个整数的二进制表示中不存在 连续的 1 。

7.1.1.3.1 方法一

class Solution {
public:
    int findIntegers(int n) {
        int tmp=n,cnt=0;
        while(tmp){
            tmp=tmp/2;
            cnt++;
        }
        //cnt记录n的二进制表示有多少位
        vector<vector<int>> dp(cnt-1,vector<int>(2,-1));
        return backtrack(n,cnt-1,true,false,dp);
    }

    int backtrack(int& n,int i,bool isLimited,bool pre1, vector<vector<int>>& dp){
        if(i==-1)
            return 1;

        if(!isLimited&&dp[i][pre1]>=0)
            return dp[i][pre1];
        
        int res=0;
        // n&(1<<i)
        int up=isLimited?(n>>i)&1:1;
        // 当前位填0
        res+=backtrack(n,i-1,isLimited&&up==0,false,dp);
        if(!pre1&&up==1)
            res+=backtrack(n,i-1,isLimited&&up==1,true,dp);
        
        if(!isLimited)
            dp[i][pre1]=res;
        return res;
    }
};

7.1.1.3.2 方法二

DP-600. 不含连续1的非负整数

class Solution {
public:
    int findIntegers(int n) {
        // dp[i]表示根节点位0，高度为i的满二叉树中个数
        vector<int> dp(31);
        dp[0]=1;
        dp[1]=2;
        for(int i=2;i<31;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }

        int res=0,pre=0;
        for(int i=29;i>=0;i--){
            // 第i位为1，可以填0
            if((n>>i)&1){
                res+=dp[i];
                cout<<i<<endl;
                if(pre==1){
                    break;
                }
                pre=1;
            }else{
                pre=0;
            }
            if(i==0){
                res++;
            }
        }
        return res;
    }
};

7.1.1.4 233. 数字 1 的个数

cnt1要作为记忆化搜索参数原因：

dp(i,cnt1)：i位前面填了cnt1个1，i及其之后不受限时含有的数字1个数

dp(n,0)=1：当前数字为1时有1个1

dp(n,1)=11：当前数字至少会有一个1，11时有两个1

class Solution {
public:
    int countDigitOne(int n) {
        string s=to_string(n);
        int m=s.size();
        vector<vector<int>> dp(m,vector<int>(m,-1));
        return backtrack(s,0,true,0,dp);

    }
    //dp[i][cnt1]填i以及之后位置时，前面已经填了cnt1个1
    int backtrack(string &s,int i,bool isLimited,int cnt1,vector<vector<int>>& dp){
        if(i==s.size())
            return cnt1;
        if(!isLimited&&dp[i][cnt1]>=0)
            return dp[i][cnt1];

        int res=0;
        int up=isLimited?s[i]-'0':9;
        for(int d=0;d<=up;d++){
            res+=backtrack(s,i+1,isLimited&&d==up,cnt1+(d==1),dp);
        }

        if(!isLimited)
            dp[i][cnt1]=res;
        return res;
    }
};

8 dp[i]表示从头到下标i的某一性质

8.1.1.1 剑指 Offer 46. 把数字翻译成字符串

9 子序列

子序列+不考虑相邻元素：选或不选
子序列+考虑相邻元素，枚举选哪个

定义dp数组,dp[i]表示到位置i为止的子序列的性质。

必须以i结尾，需要遍历dp数组得到结果

不必须以i结尾，dp数组的最后一位结果即为题目所求

9.1.1.1 300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

求解上升子序列方法：

动态规划

优化方法：

单调栈+二分优化

线段树、平衡树等数据结构优化

9.1.1.1.1 DP

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        vector<int> dp(n,1);
        int ans=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[j]<nums[i]){
                    dp[i]=max(dp[i],dp[j]+1);
                    ans=max(ans,dp[i]);
                }
            }
        }
        return ans;
    }
};

9.1.1.1.2 贪心+二分查找

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> stk;
        for(int num:nums){
            if(stk.empty()||num>stk.back())
                stk.push_back(num);
            else{
                // 找到>=num的第一个位置
                int left=0,right=stk.size()-1;
                while(left<right){
                    int mid=left+(right-left)/2;
                    if(stk[mid]<num)
                        left=mid+1;
                    else
                        right=mid;
                }
                stk[left]=num;
            }
        }
        return stk.size();
    }
};

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> stk;
        for(int num:nums){
            if(stk.empty()||num>stk.back())
                stk.push_back(num);
            else{
                // 找到>=num的第一个位置
                auto iter=lower_bound(stk.begin(),stk.end(),num);
                *iter=num;
            }
        }
        return stk.size();
    }
};

9.1.1.2 376. 摆动序列

$$
dp[i][0]表示[0:i]范围内，以nums[i]为止，最后下降的序列长度\
dp[i][1]表示[0:i]范围内，以nums[i]为止，最后上升的序列长度
$$

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        vector<vector<int>> dp(n,vector<int>(2,1));
        int ans=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]-nums[j]>0){
                    dp[i][1]=max(dp[i][1],dp[j][0]+1);
                }else if(nums[i]<nums[j]){
                    dp[i][0]=max(dp[i][0],dp[j][1]+1);
                }
                ans=max(ans,max(dp[i][1],dp[i][0]));
            }
        }
        return ans;
    }
};

$$
dp[i][0]表示[0:i]范围内，不一定以nums[i]结尾，最后下降的序列长度\
dp[i][1]表示[0:i]范围内，不一定以nums[i]结尾，最后上升的序列长度
$$

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        vector<vector<int>> dp(n,vector<int>(2,1));
        for(int i=1;i<n;i++){
            //上升
            if(nums[i]>nums[i-1]){
                dp[i][1]=max(dp[i-1][1],dp[i-1][0]+1);
                dp[i][0]=dp[i-1][0];
            }else if(nums[i]<nums[i-1]){
                dp[i][1]=dp[i-1][1];
                dp[i][0]=max(dp[i-1][0],dp[i-1][1]+1);
            }else{
                dp[i][0]=dp[i-1][0];
                dp[i][1]=dp[i-1][1];
            }
        }
        return max(dp[n-1][0],dp[n-1][1]);
    }
};

空间优化

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        int up=1,down=1;
        for(int i=1;i<n;i++){
            if(nums[i]>nums[i-1]){
                up=max(up,down+1);
            }else if(nums[i]<nums[i-1]){
                down=max(down,up+1);
            }
        }
        return max(up,down);
    }
};

贪心算法

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
    if (nums.size() < 2)
        return nums.size();
    int sign = nums[0] - nums[1];
    int count = sign != 0 ? 2 : 1;
    for (int i = 2; i < nums.size(); i++)
    {
        int cursign = nums[i - 1] - nums[i];
        if ((sign >= 0 && cursign < 0) || (sign <= 0 && cursign > 0))
        {
            sign = cursign;
            count++;
        }
    }
    return count;
    }
};

9.2 最大子段和

最大子段和问题：蛮力、递归及动态规划

Given a sequence a[1],a[2],a[3]…a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.

Max Sum杭电

主要思想：如果之前求和为正，则加上当前元素，同时每次记录当前最大值，

否则，前面求和为负，应从当前位置重新求和

错误位置，此处为正确写法

#include <iostream>
#include <vector>
using namespace std;

int main() {
    // freopen("HDU/max_sum.input", "r", stdin);
    int kase;
    cin >> kase;
    int cnt = 1;
    while (kase--) {
        int n; //每一行数据数
        int max_sum, sum;
        cin >> n >> sum;
        // cout << n << endl;
        max_sum = sum;
        int begin_pos = 1, end_pos = 1;
        int index = 1;
        int begin = 1, end = 1;
        for (int i = 1; i < n; i++) {
            int t;
            index++;
            cin >> t;
            //sum+t>=t
            if (sum + t >= 0) {
                // cout << "sum: " << sum << "   t:" << t << endl;
                sum += t;
                end_pos = index;
            } else {
                sum = t;
                begin_pos = index;
                //begin_pos=end_pos=index;
            }

            if (sum > max_sum) {
                max_sum = sum;
                begin = begin_pos;
                end = end_pos;
            }
        }
        cout << "Case " << cnt++ << ":" << endl;
        cout << max_sum << " " << begin << " " << end << endl;
        if (kase)
            cout << endl;
    }
    // system("pause");
    return 0;
}

9.3 最大子矩阵和

给定一个n*m的矩阵A，求A中的一个非空子矩阵，使这个子矩阵中的元素和最大。

其中，A的子矩阵指在A中行和列均连续的一块。

链接

思想：将二维压缩到一维

#include <cstring>
#include <iostream>
#define MAX_N 502
using namespace std;
/*
 *给定一个n*m的矩阵A，求A中的一个非空子矩阵，使这个子矩阵中的元素和最大。
 */

int data[MAX_N][MAX_N];
int main() {
    freopen("HDU/input/max_matrix.input", "r", stdin);
    int n, m; // n行，m列
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cin >> data[i][j];
        }
    }
    int max_result = data[0][0];
    int column[MAX_N], dp[MAX_N] = {0};
    // memset(dp, 0, sizeof(int) * MAX_N);
    //从i行到j行压缩到column[k]中
    for (int i = 1; i <= n; ++i) {
        memset(column, 0, sizeof(int) * MAX_N);
        for (int j = i; j <= n; ++j) {
            //对列的遍历
            for (int k = 1; k <= m; ++k) {
                column[k] += data[j][k];
                if (dp[k - 1] > 0)
                    dp[k] = dp[k - 1] + column[k];
                else
                    dp[k] = column[k];
                max_result = max(max_result, dp[k]);
            }
        }
    }
    cout << max_result << endl;    system("pause");
    return 0;
}

10 分割类DP

对于分割类型题，动态规划的状态转移方程通常并不依赖相邻的位置，而是依赖于满足分割条件的位置。

10.1.1.1 139. 单词拆分

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        int n=s.size();
        unordered_set<string> record(wordDict.begin(),wordDict.end());

        vector<int> dp(n+1);
        dp[0]=true;

        for(int i=0;i<n;i++){
            for(int j=i;j>=0;j--){
                // 取字符[j:i]，找到一个可以分割的位置便可以返回
                string tmp=s.substr(j,i-j+1);
                if(record.count(tmp)&&dp[j]){
                    dp[i+1]=true;
                    break;
                }
            }
        }
        return dp[n];
    }
};

10.1.1.2 140. 单词拆分 II

10.1.1.3 279. 完全平方数

11 股票交易类

11.1.1.1 123. 买卖股票的最佳时机 III

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        vector<int> buy(3,INT_MIN),sell(3);
        int n=prices.size();
        for(int i=1;i<=n;i++){
            for(int j=1;j<=2;j++){
                buy[j]=max(buy[j],sell[j-1]-prices[i-1]);
                sell[j]=max(sell[j],buy[j]+prices[i-1]);
            }
          
        }
        return sell[2];
    }
};

只进行过一次买操作；

进行了一次买操作和一次卖操作，即完成了一笔交易；

在完成了一笔交易的前提下，进行了第二次买操作；

完成了全部两笔交易。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int buy1 = -prices[0], sell1 = 0;
        int buy2 = -prices[0], sell2 = 0;
        for (int i = 1; i < n; ++i) {
            buy1 = max(buy1, -prices[i]);
            sell1 = max(sell1, buy1 + prices[i]);
            buy2 = max(buy2, sell1 - prices[i]);
            sell2 = max(sell2, buy2 + prices[i]);
        }
        return sell2;
    }
};

分部讨论，fl[i]表示[0:i]进行股票交易可获得最大收益

fr[i]表示[i:]进行股票交易可获得最大收益

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        vector<int> fl(n),fr(n);
        int mn=prices[0];
        for(int i=1;i<n;i++){
            fl[i]=max(fl[i-1],prices[i]-mn);
            mn=min(mn,prices[i]);
        }

        int mx=prices[n-1];
        for(int i=n-2;i>=0;i--){
            fr[i]=max(fr[i+1],mx-prices[i]);
            mx=max(prices[i],mx);
        }

        int ret=0;
        for(int i=0;i<n;i++){
            ret=max(ret,fl[i]+fr[i]);
        }
        return ret;
    }
};

11.1.1.2 188. 买卖股票的最佳时机 IV

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n=prices.size();
        vector<int> buy(k+1,INT_MIN),sell(k+1);

        for(int i=1;i<=n;i++){
            for(int j=1;j<=k;j++){
                buy[j]=max(buy[j],sell[j-1]-prices[i-1]);
                sell[j]=max(sell[j],buy[j]+prices[i-1]);
                // cout<<j<<" "<<sell[j]<<endl;
            }
        }
        return sell[k];
    }
};

11.1.1.3 309. 最佳买卖股票时机含冷冻期

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();

        vector<int> buy(n+1,INT_MIN),sell(n+1);
        buy[1]=-prices[0];

        for(int i=2;i<=n;i++){
            buy[i]=max(buy[i-1],sell[i-2]-prices[i-1]);
            sell[i]=max(sell[i-1],buy[i]+prices[i-1]);
        }
        return sell[n];
    }
};

方法二

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        vector<vector<int>> dp(n,vector<int>(2,0));
        dp[0][1]=-prices[0];
        //dp[i][0]表示第i天没有股票
        for(int i=1;i<n;i++){
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
            if(i==1)
                dp[i][1]=max(dp[0][1],-prices[1]);
            else
                dp[i][1]=max(dp[i-1][1],dp[i-2][0]-prices[i]);
        }
        return dp[n-1][0];
    }
};

11.1.1.4 714. 买卖股票的最佳时机含手续费

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n=prices.size();
        vector<int> buy(n,INT_MIN);
        vector<int> sell(n);

        buy[0]=-prices[0]-fee;
        for(int i=1;i<n;i++){
            // 第i天是否买入股票
            buy[i]=max(buy[i-1],sell[i-1]-prices[i]-fee);
            sell[i]=max(sell[i-1],buy[i]+prices[i]);
        }
        return sell[n-1];
    }
};

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n=prices.size();
        int buy=-prices[0]-fee;
        int sell=0;

        for(int i=1;i<n;i++){
            // 第i天是否买入股票
            buy=max(buy,sell-prices[i]-fee);
            sell=max(sell,buy+prices[i]);
        }
        return sell;
    }
};

class Solution {
  public:
    int maxProfit(vector<int> &prices, int fee) {
        int n = prices.size();
        vector<int> buy(n, INT_MIN), sell(n, INT_MIN);
        buy[0] = -prices[0] - fee;
        sell[0] = 0;
		
        //以第i天结尾的最大收益，到第i天的最大收益
        // int ans = 0;
        // for (int i = 0; i < n; i++) {
        //     for (int j = 0; j < i; j++) {
        //         buy[i] = max(buy[i], sell[j] - prices[i] - fee);
        //         sell[i] = max(sell[i], buy[j] + prices[i]);
        //         ans = max(ans, sell[i]);
        //     }
        // }

        for (int i = 1; i < n; i++) {
            buy[i] = max(buy[i - 1], sell[i - 1] - prices[i] - fee);
            sell[i] = max(sell[i - 1], buy[i - 1] + prices[i]);
        }
        return sell[n - 1];
    }
};

#### 1911. 最大子序列交替和

12 奇偶DP

12.1.1.1 2786. 访问数组中的位置使分数最大

class Solution2 {
  public:
    long long maxScore(vector<int> &nums, int x) {
        int n = nums.size();
        vector<long long> dp(n);
        dp[0] = nums[0];

        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] % 2 == nums[j] % 2)
                    dp[i] = max(dp[i], dp[j] + nums[i]);
                else
                    dp[i] = max(dp[i], dp[j] + nums[i] - x);
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};

class Solution {
public:
    long long maxScore(vector<int>& nums, int x) {
        int n=nums.size();
        vector<long long> dp(n,LLONG_MIN);
        vector<int> mark={-1,-1};
        dp[0]=nums[0];
        mark[nums[0]%2]=0;

        long long ans=nums[0];
        for(int i=1;i<n;i++){
            int num=nums[i];
            if(mark[0]!=-1)
                dp[i]=max(dp[i],dp[mark[0]]+nums[i]-(num%2==0?0:x));
            if(mark[1]!=-1)
                dp[i]=max(dp[i],dp[mark[1]]+nums[i]-(num%2==1?0:x));
            mark[num%2]=i;
            ans=max(ans,dp[i]);
        }
        return ans;
    }
};

不能将odd和even初始化为0，因为nums[0]是初始状态

class Solution {
public:
    long long maxScore(vector<int>& nums, int x) {
        int n=nums.size();
        long long odd=INT_MIN,even=INT_MIN;
        if(nums[0]%2==0)
            even=nums[0];
        else
            odd=nums[0];
        for(int i=1;i<n;i++){
            if(nums[i]%2==0){
                even=max(odd+nums[i]-x,even+nums[i]);
            }else{
                odd=max(odd+nums[i],even+nums[i]-x);
            }
        }
        return max(odd,even);
    }
};
class Solution {
public:
    long long maxScore(vector<int>& nums, int x) {
        int n = nums.size();

        // 初始化 f[a_0 % 2]
        const long long INF = 1e18;
        long long f[2];
        f[0] = f[1] = -INF;
        f[nums[0] % 2] = nums[0];

        // 从左到右枚举访问的终点
        long long ans = nums[0];
        for (int i = 1; i < n; i++) {
            // 套用 dp 方程
            int p = nums[i] % 2;
            long long t = max(f[p] + nums[i], f[p ^ 1] + nums[i] - x);
            f[p] = max(f[p], t);
            ans = max(ans, t);
        }
        return ans;
    }
};

13 题目

#### 198. 打家劫舍
#### 213. 打家劫舍 II（环形数组，考虑首尾连接情况）

1 动态规划DP

2 空间压缩

2.1 只与有限个变量相关

2.1.1.1 91. 解码方法

2.2 二维压缩到一维

2.2.1.1 64. 最小路径和

2.3 滚动数组

2.3.1.1 221. 最大正方形

3 二维DP

4 背包DP

4.1 0-1背包

4.2 完全背包

4.2.1.1 474. 一和零

879. 盈利计划

1049. 最后一块石头的重量 II

5 字符串编辑

5.1.1.1 10. 正则表达式匹配

6 区间DP

6.1 定义

6.2 性质

7 数位DP

7.1.1 题目

7.1.1.1 6957. 统计范围内的步进数字数目

7.1.1.2 2719. 统计整数数目

7.1.1.3 600. 不含连续1的非负整数

7.1.1.3.1 方法一

7.1.1.3.2 方法二

7.1.1.4 233. 数字 1 的个数

8 dp[i]表示从头到下标i的某一性质

8.1.1.1 剑指 Offer 46. 把数字翻译成字符串

9 子序列

9.1.1.1 300. 最长递增子序列

9.1.1.1.1 DP

9.1.1.1.2 贪心+二分查找

9.1.1.2 376. 摆动序列

9.2 最大子段和

9.3 最大子矩阵和

10 分割类DP

10.1.1.1 139. 单词拆分

10.1.1.2 140. 单词拆分 II

10.1.1.3 279. 完全平方数

11 股票交易类

11.1.1.1 123. 买卖股票的最佳时机 III

11.1.1.2 188. 买卖股票的最佳时机 IV

11.1.1.3 309. 最佳买卖股票时机含冷冻期

11.1.1.4 714. 买卖股票的最佳时机含手续费

12 奇偶DP

12.1.1.1 2786. 访问数组中的位置使分数最大

13 题目