树状数组(Binary Indexed Tree, BIT)

发表于 分类于
树状数组是一种可以动态维护序列前缀和的数据结构（单点更新，区间查询）。

0.1 树状数组

树状数组是一种可以动态维护序列前缀和的数据结构（下标从1开始）：

  • 单点更新update(i,v)：将数组i位置的数加上一个值v
  • 区间查询query(i)：查询数组[1...i]区间的区间和，即i位置的前缀和
  • lowbit(i)：得到i最低位的1以及后面的0
    原始数组为a，树状数组为bit。bit[i]存放从右往左数lowbit(i)个数， $bit[i]=\sum\limits_{k=i-lowbit(i)+1}^{i}a[k]$ 。将bit初始化为0，对于每一个数字a[i]，都对bit进行$add(i,a[i])$。

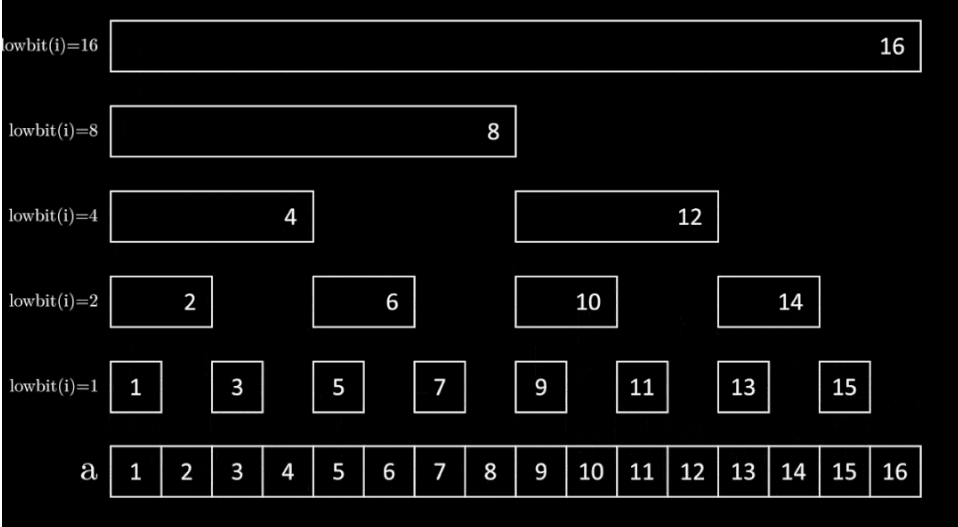
Snipaste_2023-10-02_10-59-46.png

0.2 单点更改

修改a[3]的值，需要修改每一个包含a[3]的bit[i]，当前块的位置加上当前块的长度可以跳到上面的位置
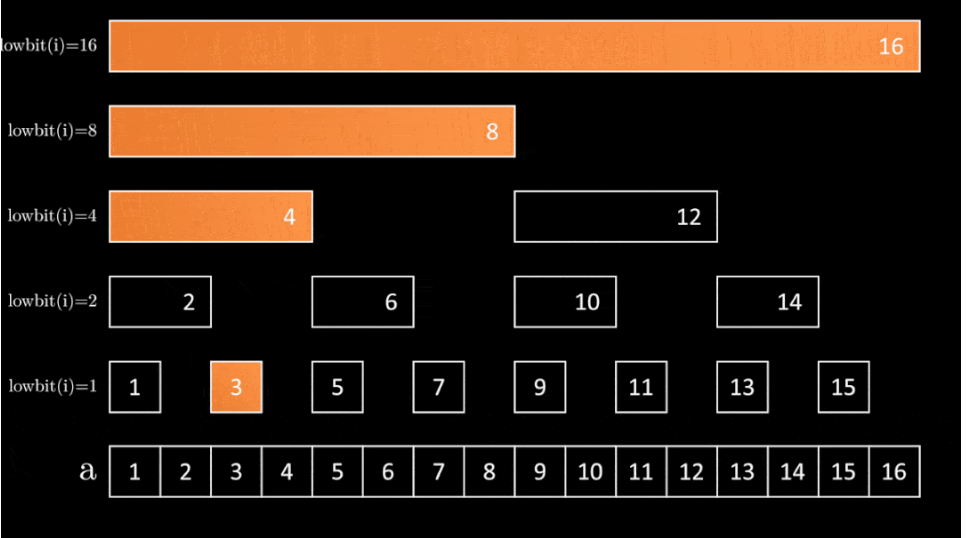
image.png

void add(int index,long long val){
	while(index<=n){
		bit[index]+=val;
		index+=lowbit(index);
	}
}

0.3 区间求和

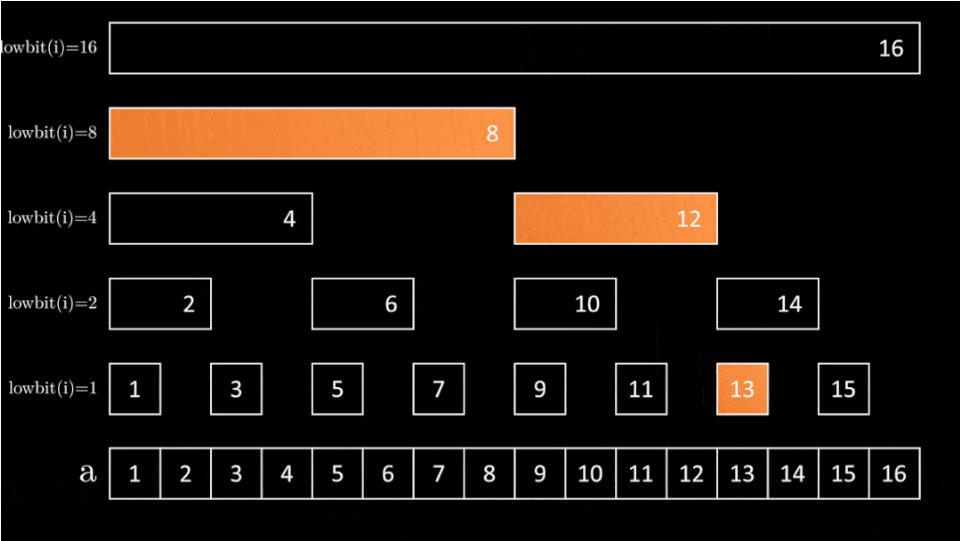
image.png

long long sum(int index){
	long long sum=0;
	while(index>0){
		sum+=bit[index];
		index-=lowbit(index);
	}
	return sum;
}

0.4 模板

0.4.1 BIT类实现

class BIT{
	private:
		int n;
		vector<int> bit;
	public:
		//总共有n个数字
		BIT(int _n){
			n=_n;
			bit=vector<int> (_n+1);
		}
		
		int lowbit(int x){
		return x&(-x);
		}
		//查询前缀和
		int query(int x){
			int sum=0;
			while(x){
				sum+=bit[x];
				x-=lowbit(x);
			}
			return sum;
		}
		//单点更新，val为a[x]变化量
		int update(int x,int val){
			while(x<=n){
				bit[x]+=val;
				x+=lowbit(x);
			}
		}
}

0.5 题单

0.5.1 315. 计算右侧小于当前元素的个数

给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

方法一：离散化树状数组

class BIT{
    private:
        int n;
        vector<int> tree;
    public:
        BIT(int _n): n(_n),tree(_n+1){}

        static int lowbit(int x){
            return x&(-x);
        }
        // 查询前缀和
        int query(int x){
            int res=0;
            while(x){
                res+=tree[x];
                x-=lowbit(x);
            }
            return res;
        }
        // 更新前缀和
        void update(int x){
            while(x<=n){
                tree[x]++;
                x+=lowbit(x);
            }
        }
};

class Solution {
public:
    vector<int> countSmaller(vector<int>& nums) {
        int n=nums.size();
        vector<int> tmp=nums;
        sort(tmp.begin(),tmp.end());
        // 将数据离散到[1:n]
        for(int &num:nums){
            num=lower_bound(tmp.begin(),tmp.end(),num)-tmp.begin()+1;
        }
        vector<int> counts(n,0);
        BIT bit(n);
        for(int i=n-1;i>=0;i--){
            counts[i]=bit.query(nums[i]-1);
            bit.update(nums[i]);
        }
        return counts;
    }
};

方法二 归并排序

class Solution1 {
  public:
    vector<int> counts;
    vector<int> tmp;
    vector<int> index;
    vector<int> tmpIndex;
    vector<int> countSmaller(vector<int> &nums) {
        int n = nums.size();
        counts.resize(n);
        tmp.resize(n);

        index.resize(n);
        iota(index.begin(), index.end(), 0);
        tmpIndex.resize(n);
        merge_sort(nums, 0, n - 1);
        return counts;
    }
    void merge_sort(vector<int> &record, int l, int r) {
        if (l >= r) {
            return;
        }

        int mid = l + (r - l) / 2;
        merge_sort(record, l, mid);
        merge_sort(record, mid + 1, r);

        // 合并两个数组
        int i = l, j = mid + 1;
        int pos = l;
        while (i <= mid && j <= r) {
            if (record[i] <= record[j]) {
                tmpIndex[pos] = index[i];
                counts[index[i]] += j - (mid + 1);
                tmp[pos++] = record[i++];
            } else {
                tmpIndex[pos] = index[j];
                tmp[pos++] = record[j++];
            }
        }
        for (int k = i; k <= mid; k++) {
            tmpIndex[pos] = index[k];
            counts[index[k]] += j - (mid + 1);
            tmp[pos++] = record[k];
        }
        for (int k = j; k <= r; k++) {
            tmpIndex[pos] = index[k];
            tmp[pos++] = record[k];
        }
        copy(tmp.begin() + l, tmp.begin() + r + 1, record.begin() + l);
        copy(tmpIndex.begin() + l, tmpIndex.begin() + r + 1, index.begin() + l);
    }
};

0.5.2 LCR 170. 交易逆序对的总数

方法一：离散化树状数组

class Solution {
public:
    vector<int> bit;
    int n;
    int reversePairs(vector<int>& record) {
        this->n=record.size();
        bit.resize(n+1);

        vector<int> tmp=record;
        sort(tmp.begin(),tmp.end());
        // 离散化数组[1,...,n]
        for(int &num:record){
            num=lower_bound(tmp.begin(),tmp.end(),num)-tmp.begin()+1;
        }

        int ans=0;
        for(int i=n-1;i>=0;i--){
            ans+=query(record[i]-1);
            update(record[i]);
        }
        return ans;
    }

    int lowbit(int x){
        return x&(-x);
    }
    int query(int index){
        int sum=0;
        while(index>0){
            sum+=bit[index];
            index-=lowbit(index);
        }
        return sum;
    }

    void update(int index){
        while(index<=n){
            bit[index]++;
            index+=lowbit(index);
        }
    }
};

方法二：归并排序

class Solution {
public:
    int reversePairs(vector<int>& record) {
        int n=record.size();
        vector<int> tmp(n);
        return merge_sort(record,tmp,0,n-1);
    }

    int merge_sort(vector<int>& record,vector<int>& tmp,int l,int r){
        if(l>=r){
            return 0;
        }

        int mid=l+(r-l)/2;
        int inv_count=merge_sort(record,tmp,l,mid)+merge_sort(record,tmp,mid+1,r);

        //合并两个数组
        int i=l,j=mid+1;
        int pos=l;
        while(i<=mid&&j<=r){
            if(record[i]<=record[j]){
                inv_count+=j-(mid+1);
                tmp[pos++]=record[i++];
            }else{
                tmp[pos++]=record[j++];
            }
        }
        for(int k=i;k<=mid;k++){
            tmp[pos++]=record[k];
            inv_count+=j-(mid+1);
        }
        for(int k=j;k<=r;k++)
            tmp[pos++]=record[k];
        copy(tmp.begin()+l,tmp.begin()+r+1,record.begin()+l);
        return inv_count;
    }
};

0.6 参考

什么是树状数组？让这个12岁年轻人为你讲解_lowbit (sohu.com)

(78条消息) 树状数组求区间最大值_LbyG的博客-CSDN博客

(78条消息) 树状数组(详细分析+应用)，看不懂打死我!_树形数组_鲜果维他命的博客-CSDN博客

树状数组（BIT）—— 一篇就够了 - Last_Whisper - 博客园 (cnblogs.com)