DFS、BFS

数据结构：二叉树，图，二维矩阵

图的遍历

• 深度优先搜索（DFS）

  检查图的连通性和无环性、关节点

• 广度优先搜索（BFS）

  检查图的连通性和无环性、求两个给定顶点间 边的数量 最少的路径

图的存储

邻接矩阵

适合于边稠密图

邻接表

适用于边数较少的稀疏图

拓扑排序

有向无环图（DAG，directed acyclic graph）

拓扑排序：对于图 G 中的任意一条有向边 (u,v)，u 在排列中都出现在 v 的前面。

m个顶点，n条边，时间复杂度O(m+n)
邻接矩阵邻接表：时间复杂度O(n+e)

算法步骤

• 搜索入度为零的顶点，加入队列

• 当队列不空时

  • 取队首元素u，加入答案
  • 将u的相邻顶点入度减1，若减为0，加入队列

• 若答案包括n个顶点，得到拓扑排序，否则有环

210. 课程表 II

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

class Solution {
private:
    // 存储有向图
    vector<vector<int>> edges;
    // 存储每个节点的入度
    vector<int> indeg;
    // 存储答案
    vector<int> result;

public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        indeg.resize(numCourses);
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
            ++indeg[info[0]];
        }

        queue<int> q;
        // 将所有入度为 0 的节点放入队列中
        for (int i = 0; i < numCourses; ++i) {
            if (indeg[i] == 0) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            // 从队首取出一个节点
            int u = q.front();
            q.pop();
            // 放入答案中
            result.push_back(u);
            for (int v: edges[u]) {
                --indeg[v];
                // 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if (indeg[v] == 0) {
                    q.push(v);
                }
            }
        }

        if (result.size() != numCourses) {
            return {};
        }
        return result;
    }
};

访问标记设置：可以通过额外的访问标记数组进行记录，或者通过修改原数组数值表明已经访问过

深度优先搜索

深度优先搜索（depth-first search, DFS）在搜索到一个新的节点时，立即堆该新节点进行遍历；深度优先搜索用先入后出的栈来实现，也可以通过递归实现。

//采用邻接表存储，递归实现
DFS(vector<vector<int>>& g,vector<bool>& visited,int cur){
    if(visited[cur]){
        return;
    }
    visited[cur]=true;
    
    for(int &next:g[cur]){
        DFS(g,visited,next);
    }
}

695. 岛屿的最大面积

递归写法：先判断是否满足条件，再进行递归，可以在访问节点时设置访问标记

class Solution {
public:
    int area=0;
    vector<int> direction={-1,0,1,0,-1};
    int m,n;
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        this->m=grid.size();
        this->n=grid[0].size();
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]){
                    area=max(area,DFS(grid,i,j));
                }
            }
        }
        return area;
    }

    int DFS(vector<vector<int>>& grid,int i,int j){
        grid[i][j]=0;
        int cnt=1;
        for(int k=0;k<4;k++){
            int x=i+direction[k],y=j+direction[k+1];
            if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1){          
                cnt+=DFS(grid,x,y);
            }
        }
        return cnt;
    }
};

栈实现

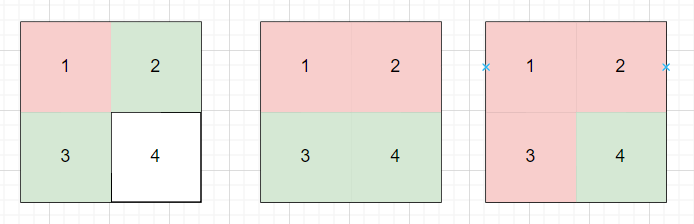
在入队时设置访问标记，如果出队时设置访问标记，可能导致多次入队，2、3出队列时分别导致4进入队列。

class Solution {
public:
    int area=0;
    vector<int> direction={-1,0,1,0,-1};
    int m,n;
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        this->m=grid.size();
        this->n=grid[0].size();
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]){
                    int local=1;
                    queue<pair<int,int>> qu;
                    grid[i][j]=0;
                    qu.push({i,j});

                    while(!qu.empty()){
                        auto [x,y]=qu.front();
                        // grid[x][y]=0;
                        qu.pop();
                        for(int k=0;k<4;k++){
                            int r=x+direction[k],c=y+direction[k+1];
                            if(r>=0&&r<m&&c>=0&&c<n&&grid[r][c]==1){
                                ++local;
                                grid[r][c]=0;
                                qu.push({r,c});
                            }
                        }
                    }
                    area=max(area,local);
                }
            }
        }
        return area;
    }
};

广度优先搜索

广度优先搜索(breadth-first search,BFS)逐层进行遍历，使用先入先出的队列进行遍历。可用于处理无权最短路径。

• 初始化：根元素入队，设置访问标记

• 当队列不为空的时候

  • 求队列长度$s_i$
  • 从队列中取$s_i$个元素，进行下一轮扩展
    • 节点未被访问过，节点入队，设置访问标记

//邻接表存储
BFS(vector<vector<int>> g){
    int n=g.size();
    vector<bool> visited(n);
    
    queue<int> qu;
    qu.push(0);
    visited[0]=true;
    
    while(!qu.empty()){
        int cur=qu.front();
        qu.pop();
        
        for(int next:g[cur]){
            if(!visited[next]){
                visited[next]=true;
                qu.push(next);
            }
        }
    }
}

$$
时间复杂度：O(n+m)，其中n为定点数，m为边数\
空间复杂度：O(n)，队列开销
$$

回溯

回溯法(backtracking)是优先搜索的一种特殊情况，常用于需要记录节点状态的深度优先搜索。排列、组合、选择类问题使用回溯法。回溯法可以对图的总状态进行修改，而非每次遍历时新建一个图来储存状态。

深度优先搜索：[修改当前节点状态]->[递归子节点]

回溯：[修改当前节点状态]->[递归子节点]->[回改当前节点状态]

• 选择k个数字构成一个排列

• 选择若干数字组成一个目标和target

• 对全部数字进行排列

78. 子集

方法一：回溯

class Solution {
    vector<vector<int>> ans;
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<int> subset;
        backtrack(nums,subset,0);
        return ans;
    }

    void backtrack(vector<int>& nums, vector<int>&subset, int start){
        if(start==nums.size()){
            ans.push_back(subset);
            return;
        }
        subset.push_back(nums[start]);
        backtrack(nums,subset,start+1);
        subset.pop_back();

        backtrack(nums,subset,start+1);

        //当前是否必须要选择一个数
        // for(int i=start;i<nums.size();i++){
        //     subset.push_back(nums[i]);
        //     backtrack(nums,subset,i+1);
        //     subset.pop_back();
        // }
    }

};

方法二：位枚举

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        int n=nums.size();
        vector<vector<int>> ans;
        vector<int> tmp;

        for(int i=0;i<(1<<n);i++){
            tmp.clear();
            for(int pos=0;pos<n;pos++){
                if((i>>pos)&1)
                    tmp.push_back(nums[pos]);
            }
            ans.push_back(tmp);
        }
        return ans;
    }
};

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

对于重复的数字要保证在结果中的相对位置一致
# 对于降重的处理
!visited[i-1]
在寻找index位置数字时，因为回溯会把visited[i-1]修改为0
visited[i]便不会被填到index的位置
而在寻找index+1位置时，由于visited[i-1]为1，则索引为i的数字被填到这一位置
寻找顺序位置，前一个相同数字填入过，则继续填入
## visited[i]
寻找逆序位置，前一个相同数字没有填入过，则继续填入

class Solution {
public:
    vector<vector<int>> ret;
    vector<bool> visited;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        visited.resize(nums.size(),false);
        sort(nums.begin(),nums.end());
        vector<int> tmp;
        backtracking(0,tmp,nums);
        return ret;
    }

    void backtracking(int index,vector<int> &tmp,vector<int> &nums){
        if(index==nums.size()){
            ret.push_back(tmp);
            cout<<"****"<<endl;
            return;
        }

        // 寻找可以填入下标Index的数字
        for(int i=0;i<nums.size();i++){
            if(visited[i]||(i>0&&nums[i]==nums[i-1]&&!visited[i-1]))
                continue;
            cout<<"index:"<<index<<" i:"<<i<<endl;
            for(auto vis:visited)
                cout<<vis<<" ";
            cout<<endl;
            visited[i]=true;
            tmp.push_back(nums[i]);
            backtracking(index+1,tmp,nums);
            tmp.pop_back();
            visited[i]=false;
        }
    }
};

934. 最短的桥

在给定的二维二进制数组 A 中，存在两座岛。（岛是由四面相连的 1 形成的一个最大组。）

现在，我们可以将 0 变为 1，以使两座岛连接起来，变成一座岛。

返回必须翻转的 0 的最小数目。（可以保证答案至少是 1 。）

广度优先搜索从一个岛屿出发不断扩展一圈，何时可以找到另外一个岛屿。前提如何保障找到扩展相应第一步时的相应初始位置。

初始时找到一个岛屿的一个点，不断向外扩展，每一层可以找到从这一点向外n步时可以到达的位置。

class Solution {
int m;
int n;
vector<int> direction={1,0,-1,0,1};
public:
    int shortestBridge(vector<vector<int>>& grid) {
        m=grid.size();
        n=grid[0].size();
        queue<pair<int,int>> q;
        bool flag=false;
        for(int i=0;i<m;i++){
            if(flag)
                break;
            for(int j=0;j<n;j++){
                if(grid[i][j]==1){
                    DFS(grid,q,i,j);
                    flag=true;
                    break;
                }
            }
        }

        int layer=0;
        while(!q.empty()){
            layer++;
            int cnt=q.size();
            // cout<<"cnt:"<<cnt<<endl;
            for(int i=0;i<cnt;i++){
                auto [x,y]=q.front();
                // cout<<x<<","<<y<<endl;
                q.pop();
                for(int k=0;k<4;k++){
                    int a=x+direction[k],b=y+direction[k+1];
                    if(a>=0&&a<m&&b>=0&&b<n){
                        if(grid[a][b]==2)
                            continue;
                    if(grid[a][b]==1){
                            // cout<<"*******"<<endl;
                             return layer;
                        }
                            grid[a][b]=2;
                            q.push({a,b});
                           
                        
                    }
                }
            }
        }
        return 0;
    }

    void DFS(vector<vector<int>> &grid,queue<pair<int,int>> &q,int x,int y){
        if(x<0||x>=m||y<0||y>=n||grid[x][y]==2)
            return;
        if(grid[x][y]==0){
            q.push({x,y});
            return;
        }
        grid[x][y]=2;
        for(int k=0;k<4;k++){
            int i=x+direction[k],j=y+direction[k+1];
            DFS(grid,q,i,j);
        }
    }
};

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

tip1

me: 用一个状态记录四周的O可以连接到的位置

在遍历所有位置，不能被四周连接到的改为‘X’

深度优先搜索

#include <iostream>
#include <vector>
using namespace std;
void dfs(vector<vector<char>> &board, vector<vector<bool>> &status, int r,
         int c);
vector<int> direction = {-1, 0, 1, 0, -1};
void solve(vector<vector<char>> &board) {
    int m = board.size(), n = board[0].size();
    vector<vector<bool>> status(m, vector<bool>(n, true));
    for (int i = 0; i < m; i++) {
        if (board[i][0] == 'O')
            dfs(board, status, i, 0);
        if (board[i][n - 1] == 'O')
            dfs(board, status, i, n - 1);
    }
    for (int j = 0; j < n; j++) {
        if (board[0][j] == 'O')
            dfs(board, status, 0, j);
        if (board[m - 1][j] == 'O')
            dfs(board, status, m - 1, j);
    }

    // for (const auto &ele : status) {
    //     for (const auto &t : ele)
    //         cout << t << " ";
    //     cout << endl;
    // }

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (status[i][j] == true && board[i][j] == 'O') {
                // cout << i << " " << j << endl;
                board[i][j] = 'X';
            }
        }
    }
}
void dfs(vector<vector<char>> &board, vector<vector<bool>> &status, int r,
         int c) {
    status[r][c] = false;
    int x, y;
    for (int k = 0; k < 4; k++) {
        x = r + direction[k];
        y = c + direction[k + 1];
        if (x >= 0 && x < board.size() && y >= 0 && y < board[0].size() &&
            board[x][y] == 'O' && status[x][y] == true) {
            // status[x][y] = false;
            // cout << x << "," << y << endl;
            dfs(board, status, x, y);
        }
    }
}
int main() {
    vector<vector<char>> board = {{'X', 'X', 'X', 'X'},
                                  {'X', 'O', 'O', 'X'},
                                  {'X', 'X', 'O', 'X'},
                                  {'X', 'O', 'X', 'X'}};
    solve(board);
    system("pause");
}

tip2

优化？？？