栈

应用

表达式求值

1. 栈实现表达式求值

如果当前运算符优先级小于等于op栈顶的运算符，则弹出两个操作数和操作符进行运算

#include <iostream>
#include <stack>
#include <string>
using namespace std;
//获取运算符优先级
int get_priority(char op) {
    switch (op) {
    case '(':
        return 0;
    case '*':
    case '/':
        return 2;
    case '+':
    case '-':
        return 1;
    default:
        return 0;
    }
}
//取两个操作数，一个运算符，进行运算
void operation(stack<int> &operand, stack<char> &op) {
    int operand2 = operand.top();
    operand.pop();
    int operand1 = operand.top();
    operand.pop();
    char t = op.top();
    op.pop();

    cout << operand1 << t << operand2 << endl;
    switch (t) {
    case '+':
        operand.push(operand1 + operand2);
        break;
    case '-':
        operand.push(operand1 - operand2);
        break;
    case '*':
        operand.push(operand1 * operand2);
        break;
    case '/':
        operand.push(operand1 / operand2);
    default:
        break;
    }
}
int main() {
    string line;
    stack<int> operand; //操作数
    stack<char> op;     //操作符
    int result;
    while (getline(cin, line)) {
        cout << line << endl;
        for (int i = 0; i < line.size(); ++i) {
            // cout << line[i] << endl;
            if (line[i] >= '0' && line[i] <= '9') {
                int num = 0;
                while (line[i] >= '0' && line[i] <= '9') {
                    num = num * 10 + line[i] - '0';
                    i++;
                }
                --i;
                operand.push(num);
                cout << "push num:" << num << endl;
                continue;
            }
            // cout << line[i] << endl;
            if (line[i] == ')') {
                while (op.top() != '(') {
                    operation(operand, op);
                }
                op.pop();
                continue;
            }

            if (!op.empty() &&
                get_priority(line[i]) <= get_priority(op.top())) {
                operation(operand, op);
            }
            op.push(line[i]);
            cout << "push op:" << line[i] << endl;
        }

        while (!op.empty()) {
            operation(operand, op);
        }
        cout << op.empty() << endl;
        cout << operand.top() << endl;
    }
    return 0;
}

2. 递归下降

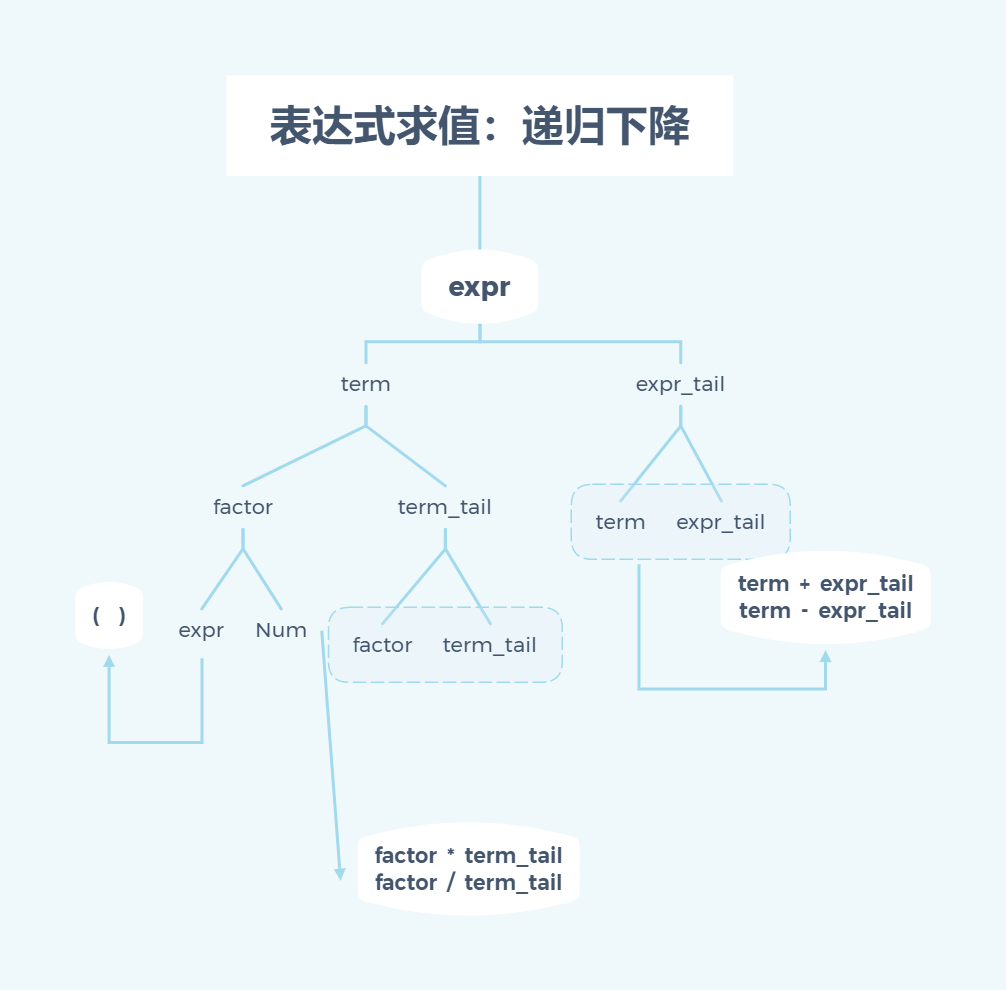
#include <stdio.h>
#include <stdlib.h>
enum { Num };
char *src = NULL;
int token;
int token_val;
int expr();
void match(int tk);
void next();
int factor() {
    int value = 0;
    if (token == '(') {
        match('(');
        value = expr();
        match(')');
    } else {
        value = token_val;
        () printf("factor value;%d\n", value);
        match(Num);
    }
    return value;
}
int term_tail(int lvalue) {
    if (token == '*') {
        match('*');
        int value = lvalue * factor();
        return term_tail(value);
    } else if (token == '/') {
        match('/');
        int value = lvalue / factor();
        return term_tail(value);
    } else {
        return lvalue;
    }
}
int term() {
    int lvalue = factor();
    return term_tail(lvalue);
}
int expr_tail(int lvalue) {
    if (token == '+') {
        match('+');
        int value = lvalue + term();
        return expr_tail(value);
    } else if (token == '-') {
        match('-');
        int value = lvalue - term();
        return expr_tail(value);
    } else {
        return lvalue;
    }
}
int expr() {
    int lvalue = term();
    return expr_tail(lvalue);
}
void match(int tk) {
    if (token != tk) {
        printf("excepted token: %d(%c), got %d(%c)\n", tk, tk, token, token);
        exit(-1);
    }
    next();
}
void next() {
    while (*src == ' ' || *src == '\t')
        src++;
    //读取token，如果是数字，则将其完整读入
    token = *src++;
    if (token >= '0' && token <= '9') {
        token_val = token - '0';
        token = Num;
        while (*src >= '0' && *src <= '9') {
            token_val = token_val * 10 + *src - '0';
            src++;
        }
        return;
    }
    printf("token:%d(%c) token_val:%d\n", token, token, token_val);
}
int main() {
    char line[100];
    while (gets(line)) {
        // printf("%s", line);
        src = line;
        next();
        printf("%d\n", expr());
    }
    return 0;
}

单调栈

单调栈通过维持栈内值的单调递增（递减）性，在O(n)的时间内处理需要大小比较的问题。

及时移除无用数据，保证栈/队列的有序性。

题目

2454. 下一个更大元素 IV（单调栈）

class Solution {

public:

    vector<int> secondGreaterElement(vector<int>& nums) {
        // using pii=pair<int,int>
        int n=nums.size();
        vector<int> ans(n,-1);
        stack<int> stk;
        priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;

        for(int i=0;i<n;i++){
            int num=nums[i];
            while(!pq.empty()&&pq.top().first<num){
                auto [_,t]=pq.top();
                pq.pop();
                ans[t]=num;
            }

            while(!stk.empty()&&nums[stk.top()]<num){
                pq.push({nums[stk.top()],stk.top()});
                stk.pop();
            }
            stk.push(i);
        }
        return ans;
    }
};