发表于 2023-05-09

双指针

区间指针

分组循环

查找符合条件的区间，寻找左右边界

2765. 最长交替子序列

class Solution {
public:
    int alternatingSubarray(vector<int>& nums) {  
        int n=nums.size();
        // 分组循环，外层循环枚举起点，内层循环扩展右侧边界
        int i=0;
        int ans=-1;
        while(i<n-1){
            if(nums[i+1]-nums[i]!=1){
                i++;
                continue;
            }
            int left=i; //记录左端点
            i++;
            while(i<n&&nums[i]==nums[left+(i-left)%2])
                i++;
            ans=max(ans,i-left);
            i--;        //回退到上一个区间最后一个位置
        }
        return ans;
    }
};

6900. 统计完全子数组的数目

class Solution {
public:
    int countCompleteSubarrays(vector<int>& nums) {
        unordered_set<int> record(nums.begin(),nums.end());
        int m=record.size();
        unordered_map<int,int> cnt;        //记录每个数字出现的个数
        
        int left=0,ans=0,n=nums.size();
        //枚举右端点
        for(int right=0;right<n;right++){
            cnt[nums[right]]++;
            while(cnt.size()==m){
                int x=nums[left++];
                if(--cnt[x]==0)
                    cnt.erase(x);
            }
            ans+=left;
        }

        return ans;
    }
};

快慢指针

floyd判圈

234. 回文链表

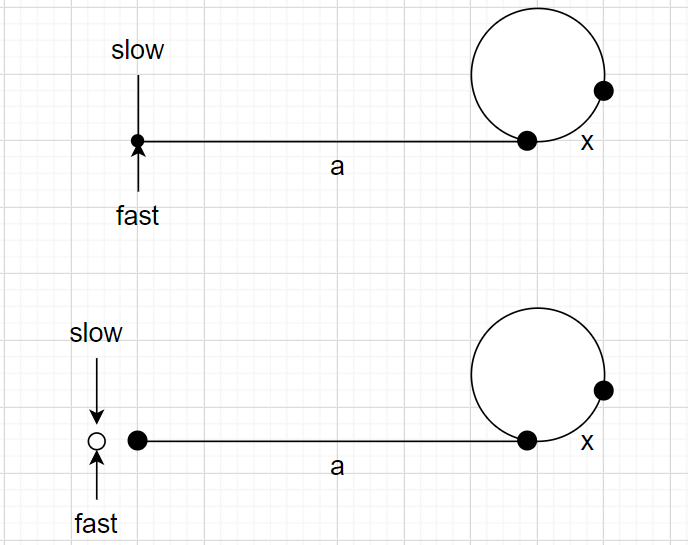
从链表第一个节点开始
$$
\begin{aligned}
r为环的长度，n为圈数 \
2(a+x-1)=(a-1)+n\times r+x \
a=n\times r -x+1
\end{aligned}
$$

从头节点（不存储数据）开始
$$
\begin{aligned}
r为环的长度，n为圈数 \
2(a+x)=a+n\times r+x \
a=n\times r -x
\end{aligned}
$$

slow，fast初始时指向同一个位置，而终止条件也是指向同一个位置，因此采用do—while循环比较好

fast遇到null停止，将判断相遇放到循环里

public ListNode detectCycle(ListNode head) {
        if(head == null || head.next == null ) {
            return null;
        }
        ListNode fast = head;
        ListNode slow = head;
        // 找到相遇点z （对应上图）
        while(true) {
            if(fast == null || fast.next == null) {
                return null;
            }
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                break;
            }
        }
        // 想到 cycle起点y （对应上图）
        slow = head;
        while(fast != slow) {
            fast = fast.next;
            slow = slow.next;
        }
        return fast;
        
    }

滑动窗口

窗口大小固定

滑动窗口，可以用来解决一些查找满足一定条件的连续区间的性质（长度等）的问题。由于区间连续，因此当区间发生变化时，可以通过旧有的计算结果对搜索空间进行剪枝，这样便减少了重复计算，降低了时间复杂度。往往类似于“请找到满足xx的最x的区间（子串、子数组）的xx”这类问题都可以使用该方法进行解决。

一般滑动窗口维护两个指针，左指针和右指针。

当窗口内的元素未达到题目条件时，右指针右移，探索未知的区间来满足条件
当窗口内的元素达到题目条件时，左指针右移，压缩区间，使窗口尽可能短得满足题目条件

首尾指针

指针分别指向首位置和尾位置，向中间移动

15. 三数之和

class Solution {
public:
    vector<vector<int>> threeSum(vector<int> &nums) {
    sort(nums.begin(), nums.end());
    vector<vector<int>> ans;
    int m, n;
    //考虑空数组情况，这里i<nums.size()-2为实际范围，这样写不用判断数组大小是否符合
    for (int i = 0; i < nums.size(); i++) {
        if (i > 0 && nums[i] == nums[i - 1])
            continue;
        m = i + 1;
        n = nums.size() - 1;
        for (; m < nums.size(); m++) {
            if (m > i + 1 && nums[m] == nums[m - 1])
                continue;
            //寻找第三个元素
            while (m < n && nums[i] + nums[m] + nums[n] > 0)
                n--;
            //比较巧妙的情况，当m==n时，说明三个数相加还是大于0的，因为已经排好序，继续向后寻找第二个数还是会大于0
            if (m == n)
                break;
            if (nums[i] + nums[m] + nums[n] == 0)
                ans.push_back(vector<int>{nums[i], nums[m], nums[n]});
        }
    }
    return ans;
}
};

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>> ans;

        int n=nums.size();

        for(int i=0;i<n-2;i++){
            if(i>0&&nums[i]==nums[i-1])
                continue;
            
            int left=i+1,right=n-1;
            while(left<right){
                while(left<right&&left>i+1&&nums[left]==nums[left-1])
                    left++;
                if(left==right)
                    break;
                
                int sum=nums[i]+nums[left]+nums[right];
                if(sum<0)
                    left++;
                else if(sum>0)
                    right--;
                else{
                    ans.push_back({nums[i],nums[left],nums[right]});
                    left++;
                    right--;
                }
            }
        }
        return ans;
    }
};

16. 最接近的三数之和

使用while循环和标记跳过重复元素

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int n=nums.size();
        int ans = nums[0] + nums[1] + nums[2];

        for(int i=0;i<n;i++){
            // 跳过相同元素
            if(i>0&&nums[i]==nums[i-1])
                continue;

            int left = i + 1, right = n - 1;
            while(left<right){
                int tmp = nums[i] + nums[left] + nums[right];
                if(tmp==target) return target;

                if(abs(target-tmp)<abs(target-ans)) ans=tmp;

                if(tmp<target){
                    int j=left+1;
                    while(j<right&&nums[j]==nums[left])
                        j++;
                    left=j;
                }else{
                    int k=right-1;
                    while(left<k&&nums[k]==nums[right])
                        k--;
                    right=k; 
                }
            }
        }
        return ans;
    }
};

18. 四数之和

class Solution {
public:
    vector<vector<int>> ans;
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        int n=nums.size();
        for(int i=0;i<n;i++){
            if(i>0&&nums[i]==nums[i-1]) continue;
            for(int j=i+1;j<n;j++){
                if(j>i+1&&nums[j]==nums[j-1])   continue;
                long cur=nums[i]+nums[j];
                // 双指针
                int left=j+1,right=n-1;
                for(;left<n;left++){
                    if(left>j+1&&nums[left]==nums[left-1])
                        continue;
                    while(left<right&&cur+nums[left]+nums[right]>target)
                        right--;
                    if(left==right)
                        break;
                    if(cur+nums[left]+nums[right]==target){
                        ans.push_back({nums[i],nums[j],nums[left],nums[right]});
                    }
                }

            }
        }
        return ans;
    }
};

方法二

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ans;

    if (nums.size() < 4)
        return ans;
    sort(nums.begin(), nums.end());
    for (int i = 0; i < nums.size(); i++)
    {
        //跳过相同的数
        if (i > 0 && nums[i] == nums[i - 1])
            continue;
        for (int j = i + 1; j < nums.size(); j++)
        {
            if (j > i + 1 && nums[j] == nums[j - 1])
                continue;
            long partSum = nums[i] + nums[j];
            int m = j + 1, n = nums.size() - 1;
            while (m < n)
            {
                if (partSum + nums[m] + nums[n] < target)
                    m++;
                else if (partSum + nums[m] + nums[n] > target)
                    n--;
                else
                {
                    ans.push_back(vector<int>{nums[i], nums[j], nums[m], nums[n]});
                    m++;
                    while (m<n&&nums[m] == nums[m - 1])
                        m++;
                    n--;
                    while (m<n&&nums[n] == nums[n + 1])
                        n--;
                }
            }
        }
    }
    return ans;
    }
};

11. 盛最多水的容器

1679. K 和数对的最大数目（哈希表）