发表于

1 差分数组、前缀和

差分数组是与前缀和数组所对应的一种逆操作，类似于求导和积分，也就是说，对差分数组求前缀和，可以得到原数组，同样的，对前缀和数组求差分，也可以得到原数组。
差分数组适用于频繁对数组区间进行增减操作，通过求前缀和得到最终数组每一元素的值。但是不适用求区间和。

前缀和、差分、树状数组、块状数组 - 力扣（LeetCode）

2 前缀和

525. 连续数组
$$
nums[L:R]=\frac{R+1-L}{2}\
s[R+1]-S[L]=\frac{R+1-L}{2}\
2s[R+1]-R=2s[L]-(L-1)
$$

class Solution {
  public:
    int findMaxLength(vector<int> &nums) {
        int n = nums.size();
        vector<int> s(n + 1);
        unordered_map<int, int> pos;        //哈希表记录和第一次出现的位置
        pos[1] = 0;

        int ans = 0;
        for (int i = 0; i < n;i++){
            s[i + 1] = s[i] + nums[i];

            if(pos.count(2*s[i+1]-i)){
                int diff = i + 1 - pos[2 * s[i + 1] - i];
                ans = max(ans, diff);
            }else{
                pos[2 * s[i + 1] - i] = i + 1;
            }
        }
        return ans;
    }
};

$$
0和1数量相同\rightarrow 1的数量-0的数量=0
$$

class Solution {
  public:
    int findMaxLength(vector<int> &nums) {
        int n = nums.size();
        vector<int> s(n + 1);
        unordered_map<int, int> pos;        //哈希表记录和第一次出现的位置
        pos[0] = 0;

        int ans = 0;
        for (int i = 0; i < n;i++){
            s[i + 1] = s[i] + (nums[i] == 1 ? 1 : -1);

            if(pos.count(s[i+1])){
                int diff = i + 1 - pos[s[i + 1]];
                ans = max(ans, diff);
            }else{
                pos[s[i + 1]] = i + 1;
            }
        }
        return ans;
    }
};

3 差分数组

差分数组对应的概念是前缀和数组，d[i]=nums[i]-nums[i-1]，d[0]=nums[0]，对差分数组求前缀和可得到原数组。

对原数组的区间[l,r]增加x时，差分数组对应的改变为：d[l]增加x，d[r+1]减少x。

d[r+1]=nums[r+1]-nums[r]，其中nums[r]增加x。

这种修改是可以叠加的，即当我们多次对原数组的不同区间施加不同的增量，我们只要按规则修改差分数组即可。

可以理解为公交车问题，在l站上车，乘坐区间[l,r]，在[r+1]站下车。

特别地，当 r 为 n 时，我们无需修改 d[r]，因为这个位置溢出了下标范围。如果求前缀和时考虑该位置，那么该位置对应的前缀和值必定为 0。读者们可以自行思考原因，以加深对差分数组的理解。

6919. 使数组中的所有元素都等于零

把子数组改成子序列要怎么做？【力扣周赛 353】_哔哩哔哩_bilibili

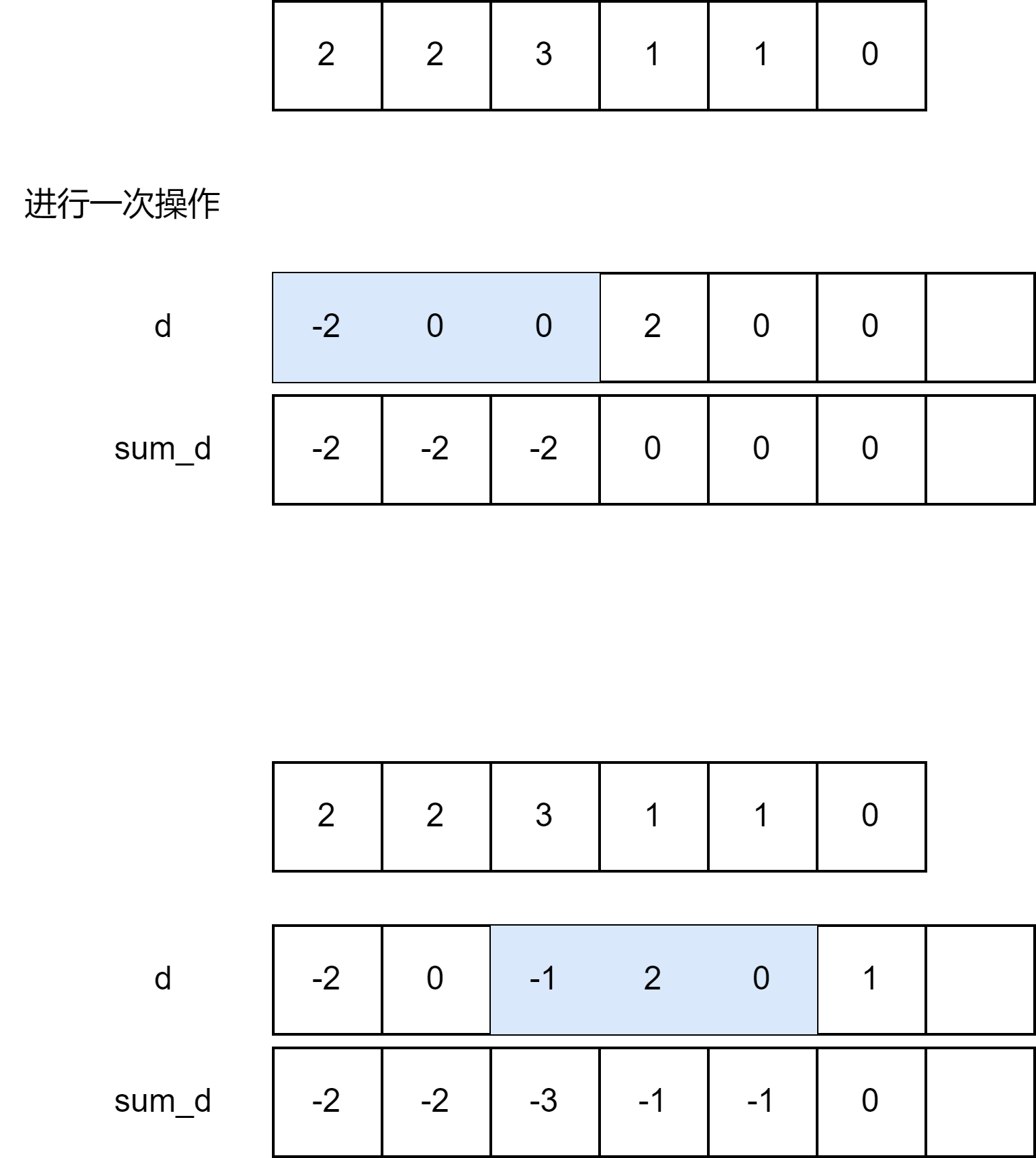
Leetcode-动态规划DP-差分数组 6919. 使数组中的所有元素都等于零.png 
class Solution {
  public:
    bool checkArray(vector<int> &nums, int k) {
        int n = nums.size();
        vector<int> d(n + 1);
        // d[0] = nums[0];

        int sum_d = 0;
        for (int i = 0; i < n;i++){
            sum_d += d[i];

            int x = sum_d+nums[i];
            if(x==0)
                continue;
            if(x<0||i+k>n)
                return false;
            sum_d -= x;
            d[i + k] += x;
        }
        return true;
    }
};

方法二

class Solution {
public:
    bool checkArray(vector<int>& nums, int K) {
        int n = nums.size();
        // 计算差分数组
        int f[n + 1];
        f[0] = nums[0];
        for (int i = 1; i < n; i++) f[i] = nums[i] - nums[i - 1];
        f[n] = -nums[n - 1];
        // 从左到右对差分数组里的每个元素进行操作
        for (int i = 0; i + K <= n; i++) if (f[i] > 0) {
            f[i + K] += f[i];
            f[i] = 0;
        }
        // 检查差分数组中是否所有元素均为 0
        for (int i = 0; i <= n; i++) if (f[i] != 0) return false;
        return true;
    }
};

★★

★★★

★★★★★

4 题目

4.1 前缀和

题目 标签
560. 和为 K 的子数组 - 力扣（LeetCode） 前缀和、哈希表(计数前缀和出现次数)