贡献法

发表于
计算每个部分的贡献

贡献法

2731. 移动机器人

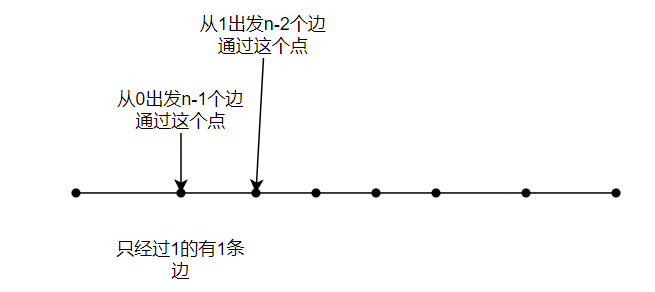
机器人碰撞可以视为机器人互相穿过对方，最后，如何计算两两机器人之间的距离之和。

方法一：贡献法： 累积计算两个点之间的线段距离和

image.png

class Solution {
public:
    const int MOD=1e9+7;
    int sumDistance(vector<int>& nums, string s, int d) {
        int n=nums.size();
        for(int i=0;i<n;i++){
            if(s[i]=='L'){
                nums[i]-=d;
            }else{
                nums[i]+=d;
            }
        }
        sort(nums.begin(),nums.end());

        long long line=0;
        long long ans=0;
        for(int i=1;i<n;i++){
            line+=n-i;
            ans=(ans+(line%MOD)*((long long)nums[i]-nums[i-1]))%MOD;
            line-=i;
        }
        return ans;
    }

};
方法二：前缀和

第i个机器人与其左侧i-1个机器人距离之和：
$$
(a[i]-a[0])+(a[i]-a[1])+…+(a[i]-a[i-1])=i*a[i]-(a[0]+a[1]+…+a[i-1])
$$

class Solution {
public:
    const int MOD=1e9+7;
    int sumDistance(vector<int>& nums, string s, int d) {
        int n=nums.size();
        vector<long long> a(n);
        for(int i=0;i<n;i++){
            if(s[i]=='L'){
               a[i]=(long long)nums[i]-d;
            }else{
                a[i]=(long long)nums[i]+d;
            }
        }
        sort(a.begin(),a.end());
        long long ans=0,sum=0;
        for(int i=0;i<n;i++){
            ans=(ans+i*a[i]-sum)%MOD;
            sum+=a[i];
        }
        return ans;
    }
};
方法三：贡献法（累积每个数字的贡献）
class Solution {
public:
    const int MOD=1e9+7;
    int sumDistance(vector<int>& nums, string s, int d) {
        int n=nums.size();
        vector<long long> result(n);
        //计算最终位置
        for(int i=0;i<n;i++){
            if(s[i]=='L'){
                result[i]=(long long)nums[i]-d;
            }else{
                result[i]=(long long)nums[i]+d;
            }
        }
        sort(result.begin(),result.end());
        long long sum=accumulate(result.begin(),result.end(),0LL);
        
        long long ans=0;
        for(int i=0;i<n;i++){
            sum-=result[i];
            ans=(ans+(sum-(n-1-i)*(long long)result[i]))%MOD;
        }
        return ans;
    }
};

2763. 所有子数组中不平衡数字之和

方法一：枚举

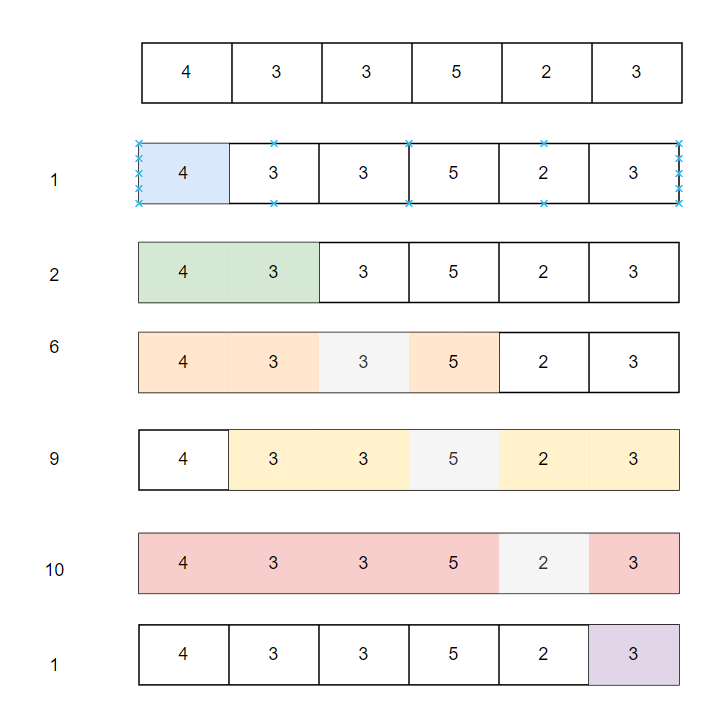
题目规定sarr[i+1] - sarr[i] > 1为不平衡数字。

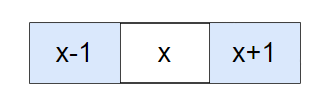
枚举子数组，i作为左侧边界，同时不断扩展右侧边界。在扩展右侧边界时，记录不平衡数字变化情况。如果x-1和x+1都存在，添加x使得不平衡数字减1。都不存在时，将使得当前数字与某一个数字构成不平衡数字。

image-20230724204058509

class Solution {
public:
    int sumImbalanceNumbers(vector<int>& nums) {
        int n=nums.size();
        bool vis[n+2];
        int ans=0;
        for(int i=0;i<n;i++){
            memset(vis,0,sizeof(vis));
            vis[nums[i]]=true;
            int cnt=0;
            for(int j=i+1;j<n;j++){
                int x=nums[j];
                // x-1 , x, x+1
                // x-1, x+1都存在，cnt-1
                // x-1, x+1都不存在,cnt+1
                if(!vis[x]){
                    cnt+=1-vis[x-1]-vis[x+1];
                    vis[x]=true;
                }

                ans+=cnt;
            }
        }
        return ans;
    }
};

方法二：贡献法

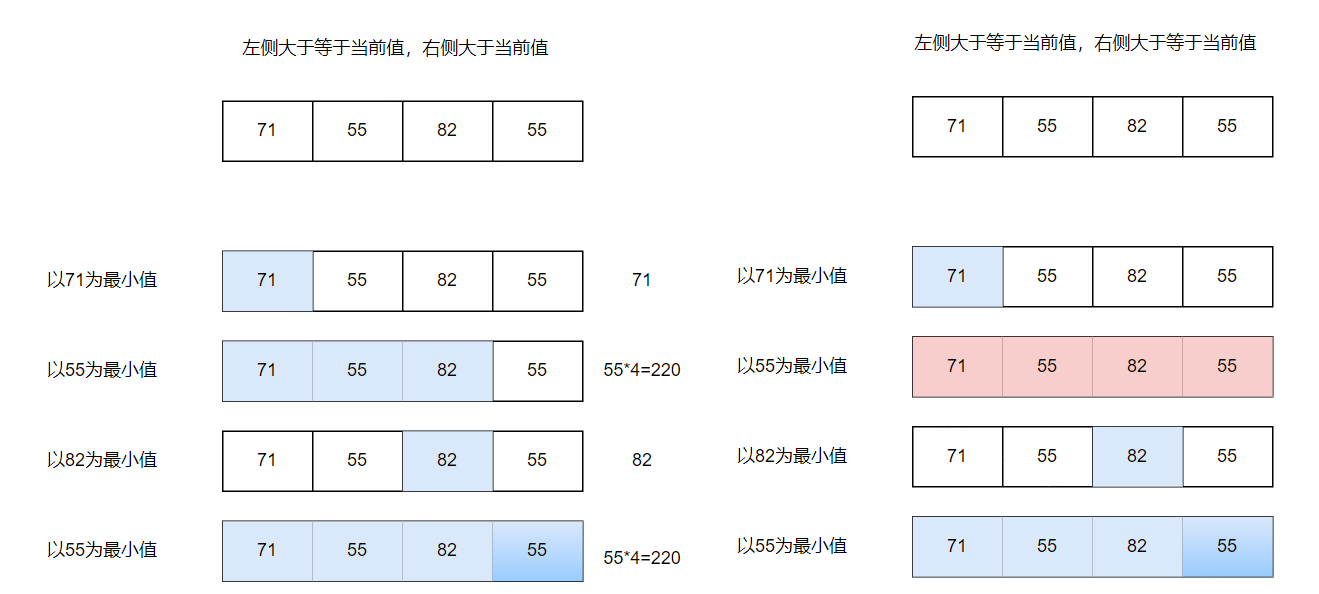
统计每个数字对不平衡数字的贡献数，x=nums[i]，子数组中如果存在x-1，则x肯定无法成为不平衡数字。同时为了避免重复统计，子数组中可以存在x+1。这考虑的是x作为不平衡数字的较大数字的贡献度。子数组左边可以包含x。同时，每个数字可能作为子数组的最小值，这种情况排序后的子数组分别有n,n-1,..,1个。

image-20230724211517496

class Solution {
  public:
    int sumImbalanceNumbers(vector<int> &nums) {
        int n = nums.size();
        // 统计每个数字对于不平衡数字的贡献
        vector<int> right(n);
        vector<int> idx(n + 1, n);

        // right[i]表示x=nums[i]，[i+1:]范围内最接近的值为x或者x-1的下标
        for (int i = n - 1; i >= 0; i--) {
            int x = nums[i];
            right[i] = min(idx[x], idx[x - 1]);
            idx[x] = i;
        }

        int ans = 0;
        idx.assign(n + 1, -1);
        for (int i = 0; i < n; i++) {
            int x = nums[i];
            int l = idx[x - 1], r = right[i];
            ans += (i - l) * (r - i);
            idx[x] = i;
        }
        return ans - n * (n + 1) / 2;
    }
};

2681. 英雄的力量

$$
a,b,c,d,e\
d作为最大值：a22+b*21+c2^0+d=s+d\
e作为最大值：a23+b*23+c21+d*20+e=2*s+d+e
$$

class Solution {
public:
// a,b,c,d,e
// a*4+b*2+c*1
// a*2+b*1
    const int MOD=1e9+7;
    int sumOfPower(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int s=0;
        int ans=0;
        for(long long num:nums){
            ans=(((s+num)*num%MOD)*num+ans)%MOD;
            s=(s*2+num)%MOD;
        }
        return ans;
    }
};

907. 子数组的最小值之和

不限制右侧可以等于的情况产生重复计算

image-20230725223937045

class Solution {
  public:
    const int MOD = 1e9 + 7;
    int sumSubarrayMins(vector<int> &arr) {
        int n = arr.size();

        // right[i]表示[i:]右侧 小于等于arr[i]的最近位置
        stack<int> stk;
        vector<int> right(n, n);

        for (int i = n - 1; i >= 0; i--) {
            // 栈顶为大值
            while (!stk.empty() && arr[stk.top()] > arr[i]) {
                stk.pop();
            }
            if (!stk.empty()) {
                right[i] = stk.top();
            }
            stk.push(i);
        }

        int ans = 0;
        while (!stk.empty())
            stk.pop();
        // 左侧小于arr[i]的最近位置
        for (long i = 0; i < n; i++) {
            while (!stk.empty() && arr[stk.top()] >= arr[i]) {
                stk.pop();
            }
            int l = stk.empty() ? -1 : stk.top();
            int r = right[i];
            ans = (ans + (i - l) * (r - i) * arr[i]) % MOD;
            stk.push(i);
        }
        return ans;
    }
};

1856. 子数组最小乘积的最大值

先去模再比较最大值会出现问题，11%10=1，9%10=9，但实际是11更大。

class Solution {
public:
    const int MOD=1e9+7;
    int maxSumMinProduct(vector<int>& nums) {
        int n=nums.size();
        // right[i]表示i下标右侧小于nums[i]的最近位置
        vector<int> right(n,n);
        stack<int> stk;
        for(int i=n-1;i>=0;i--){
            while(!stk.empty()&&nums[stk.top()]>=nums[i])
                stk.pop();
            if(!stk.empty())
                right[i]=stk.top();
            stk.push(i);
        }

        while(!stk.empty())
            stk.pop();
        
        // 计算前缀和
        vector<long long> sum(n+1);
        sum[0]=0;
        for(int i=1;i<=n;i++){
            sum[i]=sum[i-1]+nums[i-1];
        }
        
        long long ans=0;
        for(int i=0;i<n;i++){
            while(!stk.empty()&&nums[stk.top()]>=nums[i])
                stk.pop();
            int l=stk.empty()?-1:stk.top();
            int r=right[i];
            stk.push(i);

            ans=max(ans,nums[i]*(sum[r]-sum[l+1]));
            // int cur=(nums[i]*(sum[r]-sum[l+1]))%MOD;
            // ans=max(ans,cur);
        }
        return ans%MOD;
    }
};

2104. 子数组范围和

单调栈+贡献法，分别计算每个数作为最大值、最小值的贡献

class Solution {
public:
    long long subArrayRanges(vector<int>& nums) {
        int n=nums.size();
        // 贡献法，枚举每个数字x=nums[i]分别作为最小值，最大值的贡献度
        vector<int> minRight(n,n),minLeft(n,-1);
        vector<int> maxRight(n,n),maxLeft(n,-1);

        stack<int> minStk,maxStk;

        for(int i=n-1;i>=0;i--){
            // x=nums[i]，找到右侧<=x的第一个位置
            while(!minStk.empty()&&nums[minStk.top()]>nums[i])
                minStk.pop();
            if(!minStk.empty())
                minRight[i]=minStk.top();
            minStk.push(i);

            // x=nums[i]，找到右侧>=x第一个位置
            while(!maxStk.empty()&&nums[maxStk.top()]<nums[i])
                maxStk.pop();
            if(!maxStk.empty())
                maxRight[i]=maxStk.top();
            maxStk.push(i);
        }

        minStk=stack<int>();
        maxStk=stack<int>();

        for(int i=0;i<n;i++){
            // x=nums[i]，找到左侧<x的第一个位置
            while(!minStk.empty()&&nums[minStk.top()]>=nums[i])
                minStk.pop();
            if(!minStk.empty())
                minLeft[i]=minStk.top();
            minStk.push(i);

            // x=nums[i]，找到左侧>x第一个位置
            while(!maxStk.empty()&&nums[maxStk.top()]<=nums[i])
                maxStk.pop();
            if(!maxStk.empty())
                maxLeft[i]=maxStk.top();
            maxStk.push(i);
        }

        long long ans=0;

        for(long long i=0;i<n;i++){
            long long minP=(i-minLeft[i])*(minRight[i]-i)*nums[i];
            long long maxP=(i-maxLeft[i])*(maxRight[i]-i)*nums[i];
            ans=ans-minP+maxP;
        }
        return ans;
    }
};

2281. 巫师的总力量和

求的是子数组的和*最小值，然后所有子数组的情况再进行求和

$$
\begin{aligned}
&sum是strength的前缀和，ss是sum的前缀和\
&对于[L+1,R-1]范围内，和为sum[R]-sum[L-1]\
&[L+1,R-1]范围内的所有子数组：\ \ \
&\sum_{p=L+1}{i}\sum_{q=i}{R-1}(sum[q+1]-sum[p])\
&=(i-L)\sum_{q=i}{R-1}sum[q+1]-(R-i)\sum_{p=L+1}{i}sum[p]\
&=(i-L)[sum[i+1]…sum[R]]-(R-i)[sum[L+1]…sum[i]]\
&=(i-L)(ss[R+1]-ss[i+1])-(R-i)(ss[i+1]-ss[L+1])
\end{aligned}
$$

class Solution {
  public:
    const int MOD = 1e9 + 7;
    int totalStrength(vector<int> &strength) {
        int n = strength.size();
        vector<int> right(n, n);
        stack<int> stk;
        for (int i = n - 1; i >= 0; i--) {
            // 右侧比x=nums[i]小的数的最近下标
            while (!stk.empty() && strength[stk.top()] > strength[i])
                stk.pop();
            if (!stk.empty())
                right[i] = stk.top();
            stk.push(i);
        }
        vector<int> sum(n + 1);
        for (int i = 1; i <= n; i++) {
            sum[i] = (sum[i - 1] + strength[i - 1]) % MOD;
        }

        // 计算前缀和的前缀和
        vector<long long> ss(n + 2);
        ss[0] = sum[0];
        for (int i = 1; i <= n + 1; i++) {
            ss[i] = (ss[i - 1] + sum[i - 1]) % MOD;
        }

        stk = stack<int>();
        int ans = 0;
        for (int i = 0; i < n; i++) {
            while (!stk.empty() && strength[stk.top()] >= strength[i])
                stk.pop();

            int l = stk.empty() ? -1 : stk.top();
            int r = right[i];
            stk.push(i);
            // [l+1,r-1]，取模后，两个ss相减可能为负值
            long long tmp = (i - l) * (ss[r + 1] - ss[i + 1]) -
                            (r - i) * (ss[i + 1] - ss[l + 1]);
            ans = (ans + (tmp % MOD) * strength[i]) % MOD;
        }
        return (ans+MOD)%MOD;
    }
};

891. 子序列宽度之和

分清每次枚举数字时的单个状态变化，以及需要求的答案总状态

$$
\begin{aligned}
a,b,c,d,e\
以d作为最大值的贡献：s&=22*|d-a|+21*|d-b|+2^0*|d-c|\
以e作为最大值的贡献：s’&=23*|e-a|+22*|e-b|+21*|e-c|+20*|e-d|\
&=2*(22*|d-a|+21*|d-b|+2^0*|d-c|)\
&\quad +23*|e-d|+22*|e-d|+21*|e-d|+20*|e-d|\
&=2s+(23+22+21+20)|e-d|
\end{aligned}
$$

class Solution {
public:
    const int MOD=1e9+7;
    int sumSubseqWidths(vector<int>& nums) {
        int n=nums.size();
        sort(nums.begin(),nums.end());

        long long total=0,s=0;
        int ans=0;
        int pre=nums[0];
        for(int num:nums){
            s=(2*s+total*(num-pre))%MOD;
            ans=(ans+s)%MOD;
            total=(2*total+1)%MOD;
            pre=num;
        }
        return ans;
    }
};

方法二：考虑多少个e减去前面数的和

class Solution {
    public int sumSubseqWidths(int[] nums) {
        Arrays.sort(nums);
        int MOD = (int)1e9+7;
        long res = 0;
        long sum = 0, total = 0;
        // sum计算当前元素num之前元素作为最小元素时的元素和， total计算当前元素num作为最大元素时的个数和
        for(long num : nums){
            res = (res + num % MOD * total  - sum) % MOD;
            sum = (sum * 2 + num) % MOD;
            total = (total * 2 + 1) % MOD;
        }
        return (int)res;
    }
}