树：二叉树

发表于
树的遍历；最近公共祖先(LCA)；树上倍增

二叉树

struct TreeNode { int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

完全二叉树是由满二叉树而引出来的，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

树的遍历：先根、中根、后根、层次

先根遍历(preorder)

递归

void preorder(TreeNode* root){
    if(!root)
        return;
    ans.push_back(root->val);
    preorder(root->left);
    preorder(root->right);
}

迭代


vector<int> preorderTraversal(TreeNode* root) {
    vector<int> ans;
    stack<TreeNode*> stk;
    while(!stk.empty()||root){
        // 沿着左子树下降
        while(root){
            ans.push_back(root->val);
            stk.push(root);
            root=root->left;
        }
        root=stk.top();
        stk.pop();
        root=root->right;
    }
    return ans;
}

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode *> stk;
        vector<int> ans;
        while(root!=nullptr||!stk.empty()){
            while(root==nullptr&&!stk.empty()){
                root=stk.top();
                root=root->right;    
                stk.pop();
            }
            if(root){
            ans.push_back(root->val);
            stk.push(root);
            root=root->left;}
        }
        return ans;
    }
};

//N叉树
class Solution {
public:
    vector<int> preorder(Node* root) {
        vector<int> ans;
        if(root==nullptr)
            return ans;
        stack<Node*> stk;
        stk.push(root);
        while(!stk.empty()){
            Node* cur=stk.top();
            stk.pop();
            ans.push_back(cur->val);

            for(int i=cur->children.size()-1;i>=0;i--){
                stk.push(cur->children[i]);
            }
        }
        return ans;
    }
};

589. N 叉树的前序遍历 - 力扣（LeetCode）

Mirros遍历

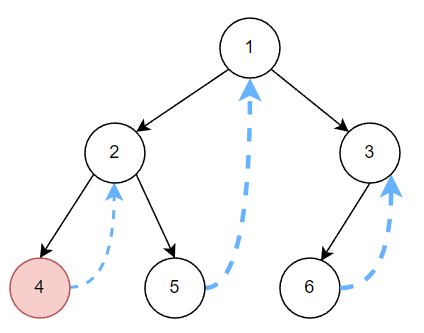
vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        TreeNode* predesessor;

        while(root){
            if(root->left!=nullptr){
                predesessor=root->left;
                while(predesessor->right&&predesessor->right!=root){
                    predesessor=predesessor->right;
                }

                if(predesessor->right!=root){
                    predesessor->right=root;
                    ans.push_back(root->val);
                    root=root->left;
                }else{
                     predesessor->right=nullptr;
                    root=root->right;
                   
                }
            }else{
                ans.push_back(root->val);
                root=root->right;
            }
        }
        return ans;
    }

中根遍历(inorder)

二叉树的中序遍历 - 二叉树的中序遍历 - 力扣（LeetCode）

递归

inorder(root){
    if(!root)
        return;
    inorder(root->left);
    处理根结点
    inorder(root->right);
}

时间复杂度：O(n)，其中 n为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。

空间复杂度：O(n)。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n)的级别。

迭代

沿着左侧路径下降，访问该结点，转到右侧路径

vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> stk;

        while(root||!stk.empty()){
            //沿着左子树下降
            while(root){
                stk.push(root);
                root=root->left;
            }
            //弹出最后的左子节点，访问，接下来访问右子树
            root=stk.top();
            stk.pop();
            ret.push_back(root->val);
            root=root->right;
        }
        return ret;
    }

时间复杂度：O(n)，其中 n为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。

空间复杂度：O(n)。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n)的级别。

Morris遍历

mirros记录了一条返回路径，可以通过该路径访问到下一个应该访问的节点

root沿着左子树下降，并记录左子树最右侧节点返回到当前节点的路径

访问完root的左子树后，应该返回到root

如果左子树的最右侧节点已经指向了自身，说明左子树已经遍历结束，当前遍历根节点，转向右子树

image-20230728171105746

vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        TreeNode *predesessor;

        while(root!=nullptr){
            //左子树不为空，寻找左子树的最右结点
            if(root->left!=nullptr){
                predesessor=root->left;
                while(predesessor->right!=nullptr&&predesessor->right!=root){
                    predesessor=predesessor->right;
                }
				
                //判断最右结点是否访问过
                if(predesessor->right!=root){
                    predesessor->right=root;
                    root=root->left;
                }
                else{
                    ret.push_back(root->val);
                    predesessor->right=nullptr;
                    root=root->right;
                }

            }
            //左子树为空
            else{
                ret.push_back(root->val);
                root=root->right;
            }
        }
        return ret;
    }

后根遍历

递归

inorder(root){
    if(!root)
        return;
    inorder(root->left);
    inorder(root->right);
    处理根结点
}

迭代

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        stack<pair<TreeNode*,int>> stk;
        
        while(root||!stk.empty()){
            //沿着左子树下降
            while(root){
                stk.push({root,-1});
                root=root->left;
            }
			//auto [root,mark]=stk.top()，错误，新建了一个临时root变量
            root=stk.top().first;
            int mark=stk.top().second;
            stk.pop();
            //右子树还未访问
            if(mark==-1){
                stk.push({root,0});
                root=root->right;
            }else{
                ans.push_back(root->val);
                //下面将指针置为null
                root=nullptr;
            }
        }
        return ans;
    }
};
class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        stack<TreeNode *> stk;
        TreeNode *prev = nullptr;
        while (root != nullptr || !stk.empty()) {
            while (root != nullptr) {
                stk.emplace(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            //root的right节点为其右子节点，则右子树已经遍历过
            if (root->right == nullptr || root->right == prev) {
                res.emplace_back(root->val);
                prev = root;
                root = nullptr;
            } else {
                stk.emplace(root);
                root = root->right;
            }
        }
        return res;
    }
};

Mirros遍历

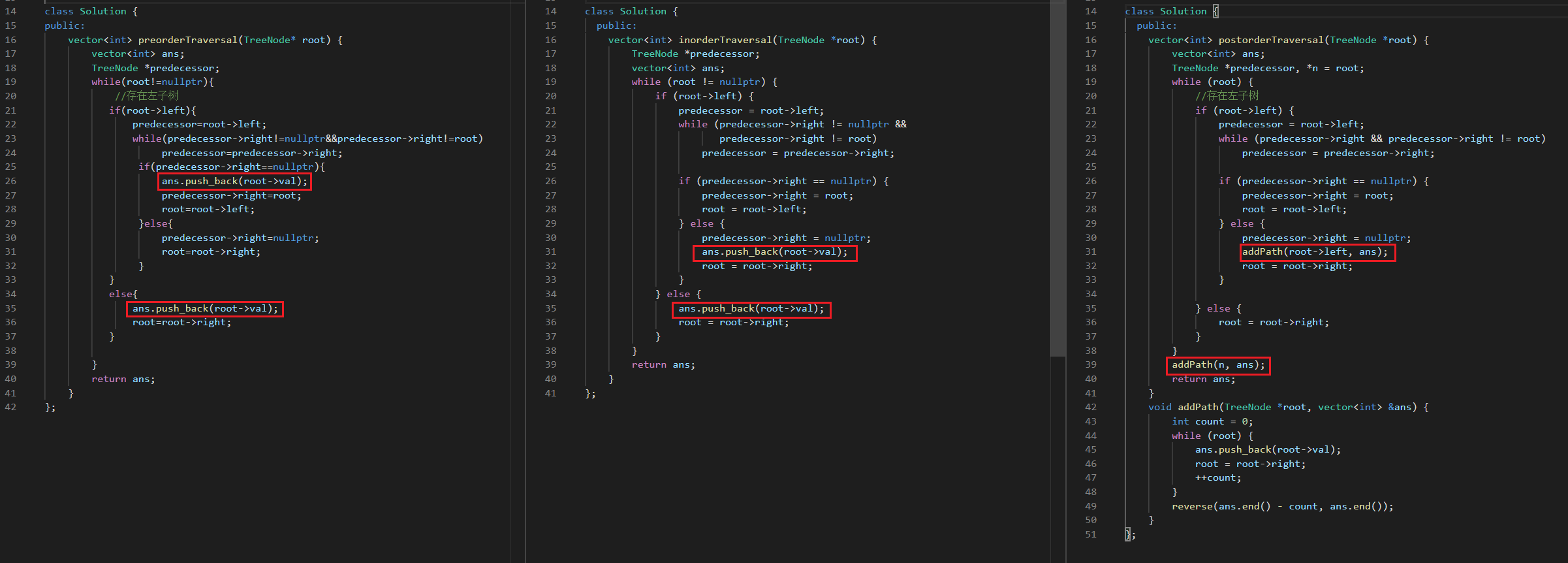
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        TreeNode* n=root;
        while(root){
            if(root->left){
                TreeNode* predecessor=root->left;
                while(predecessor->right&&predecessor->right!=root){
                    predecessor=predecessor->right;
                }

                if(predecessor->right==nullptr){
                    predecessor->right=root;
                    root=root->left;
                }else{
                    predecessor->right=nullptr;
                    addPath(root->left,ans);
                    root=root->right;
                }
            }else{
                root=root->right;
            }
        }
        addPath(n,ans);
        return ans;
    }
    void addPath(TreeNode* root,vector<int> &ans){
        int count=0;
        while(root){
            ans.push_back(root->val);
            root=root->right;
            count++;
        }
        reverse(ans.end()-count,ans.end());
    }
};

Mirros遍历比较

202203231116998.png
image-20220323112113166

LCA(latest common ancestor)

236. 二叉树的最近公共祖先方法一

class Solution {
public:
    TreeNode *ans;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //当前节点满足，记录下答案
        if(DFS(root,p)&&DFS(root,q)){
            ans=root;
        }else{
            return NULL;
        }
		//左侧不满足，查找右侧
        if(lowestCommonAncestor(root->left,p,q)==NULL){
            lowestCommonAncestor(root->right,p,q);
        }
        return ans;
    }

    // 从root是否可以到达target
    bool DFS(TreeNode* root,TreeNode *target){
        if(root==NULL){
            return false;
        }
        if(root==target){
            return true;
        }
        return DFS(root->left,target)||DFS(root->right,target);
    }
};

方法二

//先递归，再判断
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL)
            return NULL;
        TreeNode*l=lowestCommonAncestor(root->left,p,q);
        if(l!=NULL)
            return l; 
        TreeNode*r= lowestCommonAncestor(root->right,p,q);
        if(r!=NULL)
            return r;

        if(check(root,p)&&check(root,q))
            return root;
        return NULL;
    }

    bool check(TreeNode* root,TreeNode *p){
        if(root==NULL)
            return false;
        if(root==p)
            return true;
        return check(root->left,p)||check(root->right,p);
    }
};

方法三

class Solution {
public:
  TreeNode *ans;
  TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {
      DFS(root,p,q);
      return ans;
  }
  bool DFS(TreeNode *root, TreeNode *p, TreeNode *q){
    if(root==nullptr){
        return false;
    }
    bool lson = DFS(root->left, p, q);
    bool rson = DFS(root->right, p, q);

    if((lson&&rson)||((root==p||root==q)&&(lson||rson))){
        ans = root;
    }

    return lson||rson||(root == p || root == q);
  }
};
class Solution {
public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {
        if (root == nullptr || root == p || root == q)
            return root;
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if (left && right)
            return root;
        return left ? left : right;
    }
};

方法四 哈希表，记录节点父节点

class Solution {
public:
    unordered_map<int,TreeNode*> fa;        //记录节点的父节点
    unordered_set<TreeNode*> visited;       
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        fa[root->val]=NULL;
        DFS(root);

        while(p!=NULL){
            visited.insert(p);
            p=fa[p->val];
        }

        while(q!=nullptr){
            if(visited.count(q))
                return q;
            q=fa[q->val];
        }
        return nullptr;
    }

    void DFS(TreeNode* root){
        if(root->left!=NULL){
            fa[root->left->val]=root;
            DFS(root->left);
        }

        if(root->right!=NULL){
            fa[root->right->val]=root;
            DFS(root->right);
        }
    }
};

树上倍增

1483. 树节点的第 K 个祖先
$$
dp[i][j]表示节点i的第2j个祖先节点，即从节点i跳2j步到达的节点\
dp[i][j]=dp [\textbf{ dp[i][j-1] } ] [j-1]
$$

求节点node的第k个节点：
$k=13=(1101)_2$，可以先往上跳 8步，再往上跳 4步和 1 步；也可以先往上跳 1 步，再往上跳 4 步和 8步。

class TreeAncestor {
public:
    vector<vector<int>> dp;
    TreeAncestor(int n, vector<int>& parent) {
        int m=32-__builtin_clz(n);//n的二进制长度
        // dp[i][j]表示i节点的2**j个祖先
        dp.resize(n,vector<int>(m,-1));

        for(int i=0;i<n;i++){
            dp[i][0]=parent[i];
        }

        for(int i=1;i<m;i++){
            for(int x=0;x<n;x++){
                int p=dp[x][i-1];
                if(p!=-1)
                    dp[x][i]=dp[p][i-1];
            }
        }
    }
    
    int getKthAncestor(int node, int k) {
        int m=32-__builtin_clz(k);
        for(int i=0;i<m;i++){
            if((k>>i)&1){
                node=dp[node][i];
                if(node<0)
                    return node;
            }
        }
        return node;
    }
};

最近公共祖先（LCA）：通过树上倍增求

1483. 树节点的第 K 个祖先 - 力扣（LeetCode）

首先使a和b处于同一深度

  • 若跳$2^i$步后，x==y(a和b的LCA和以上节点都相同)，则LCA为当前节点或者下面节点，不跳
  • 若跳$2^i$步后，x!=y，则说明还未到达最近祖先节点，进行跳操作
class TreeAncestor {
  public:
    // 无向无环图，有n-1条边
    vector<vector<int>> pa;
    vector<int> depth;
    TreeAncestor(vector<vector<int>> &edges) {
        int n = edges.size() + 1;
        int m = 32 - __builtin_clz(n);	//n的二进制长度
        pa.resize(n, vector<int>(m, -1));
        depth.resize(n);

        // 根据边建图
        vector<vector<int>> g(n);
        for (auto [x, y] : edges) {
            g[x].push_back(y);
            g[y].push_back(x);
        }

        // dfs遍历树，求每一个节点对应的深度
        function<void<int, int>> dfs = [&](int x, int fa) {
            pa[x][0] = fa;
            for (int y : g[x]) {
                if (y != fa) {
                    depth[y] = depth[x] + 1;
                    dfs(y, x);
                }
            }
        };
        dfs(0, -1);

        // 倍增算法
        for (int i = 1; i < m; i++) {
            for (int x = 0; x < n; x++) {
                if (int p = pa[x][i - 1]; p != -1)
                    pa[x][i + 1] = pa[p][i];
            }
        }
    }

    // node节点向上跳k步到达的节点
    int getKthAncestor(int node, int k) {
        int m = 32 - __builtin_clz(k);
        for (int i = 0; i < m; i++) {
            if ((k >> i) & 1) {
                node = pa[node][i];
                if (node < 0)
                    break;
            }
        }
        return node;
    }
    
    int get_kth_ancestor(int node, int k) {
        for (; k; k &= k - 1)
            node = pa[node][__builtin_ctz(k)];
        return node;
    }

    // 返回x和y的最近公共祖先（节点编号从0开始）
    int get_lca(int x, int y) {
        if (depth[x] > depth[y])
            swap(x, y);
        // 使y和x处于同一深度
        y = getKthAncestor(y, depth[y] - depth[x]);

        if (y == x)
            return x;

        for (int i = pa[x].size() - 1; i >= 0; i--) {
            int px = pa[x][i], py = pa[y][i];
            if (px != py) {
                x = px;
                y = py;
            }
        }
        return pa[x][0];
    }
};

OptimalBST（最优搜索二叉树）

二叉查找树(Binary Search Tree,BST) 是一种特殊的二叉树：对于每个父节点，其左子节点的值小于等于父节点的值，其右子节点的值大于等于父节点的值。可以在$O(nlogn)$的时间内查找一个值是否存在。

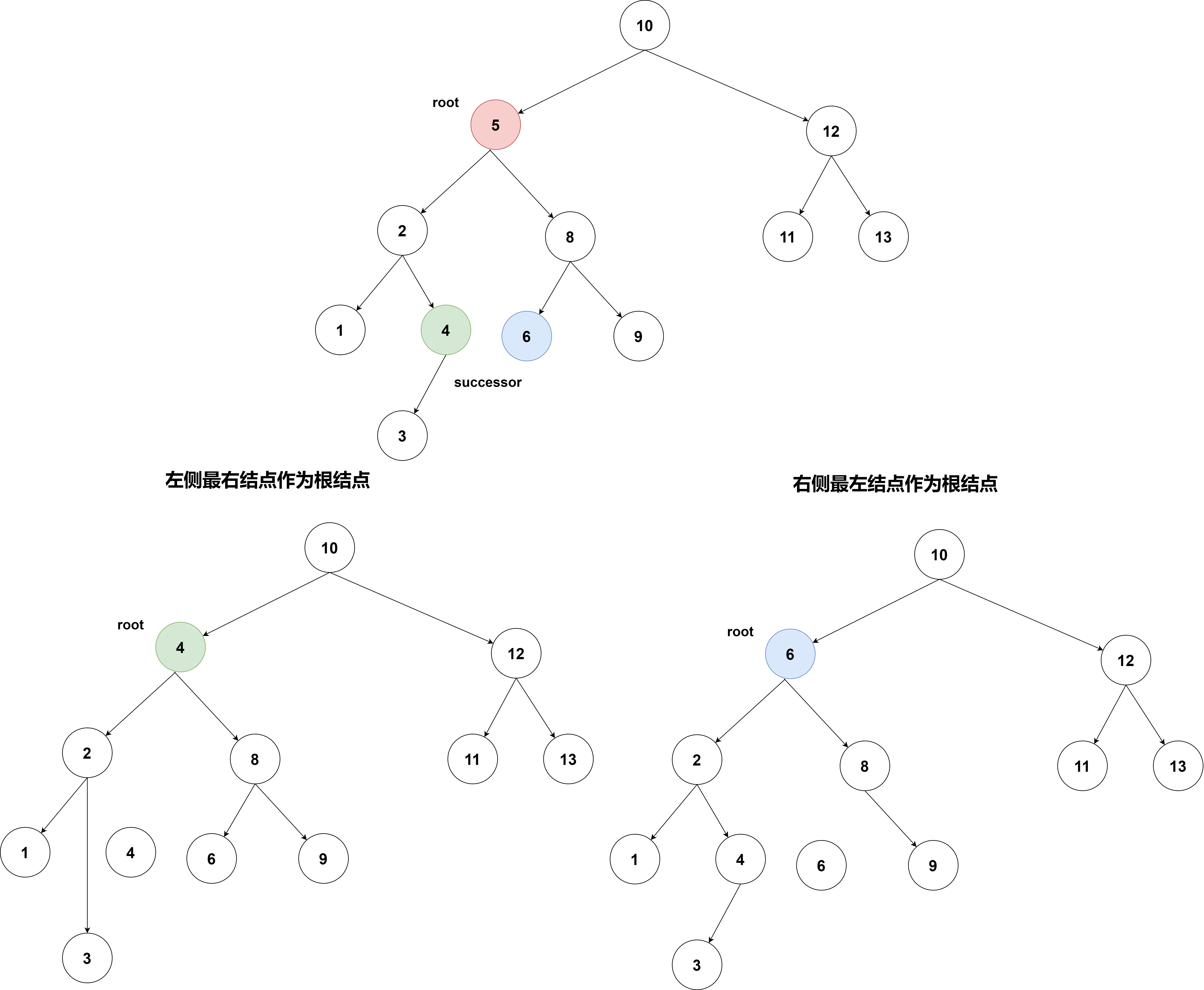
class BST {
    struct TreeNode {
        int val;
        TreeNode *left, *right;
    };

    class Solution {
      public:
        TreeNode *deleteNode(TreeNode *root, int key) {
            if (root == nullptr) {
                return root;
            }

            if (root->val < key) {
                root->right = deleteNode(root->right, key);
            } else if (root->val > key) {
                root->left = deleteNode(root->left, key);

            } else {
                // 没有右子树
                if (root->right == nullptr) {
                    return root->left;
                }
                // 没有左子树
                if (root->left == nullptr) {
                    return root->right;
                }
                // 存在左右子树，寻找左子树的最大节点
                TreeNode *successor = root->left;
                while (successor->right) {
                    successor = successor->right;
                }
                // 从root中删除successor节点

                // 保留源节点
                //  root->left = deleteNode(root->left, successor->val);
                //  successor->left = root->left;
                //  successor->right = root->right;
                //  return successor;

                // 复制原节点值
                root->val = successor->val;
                root->left = deleteNode(root->left, root->val);
            }
            return root;
        }
    };
};

删除二叉搜索树中的节点 - 删除二叉搜索树中的节点 - 力扣（LeetCode）

  • root为空，未找到值为key的节点

  • root->val>key，继续在左子树中寻找

  • root->val< key，继续在右子树中寻找

  • root->val == key ，root为要删除的节点

    • root为叶节点后者只有左右子树中的一个
    • root有左右子树，在左子树中寻找前驱节点（在右子树中寻找后继节点），从左子树中删除前驱节点，用前驱节点替换root节点

leetcode图解-删除二叉树节点.png