常量指针与指针常量
|

#include <stdio.h> |

sequence
[1,2,3]
odds=[3,5,7,9,11]
list(range(1,3))
[1,2]
[odds[i] for i in range(1,3)]
[5,7]
sum([1,2,3])=6
sum([[1,2],[3]],[])=[1,2,3]


函数参数加*号,代表将多个参数组装成列表
数组前面加参数,代表把数组拆分成多个逗号分割的变量,类似js中的展开符号.
def add(x,y): |
tuple
immutable sequences
Lecture18
scanf
读取空格、换行符
#include <stdio.h> |


int a[10]; 声明,未初始化
int a[10]={0}; //全部初始化为0
int a[10]={1}; //第一个元素为1,后面初始化为0
#include <stdio.h> |

结果输出10
#include <stdio.h> |
sizeof返回占用的字节数,但数组作为参数传递时不能有效计算占用的字节数,需加参数指明占用的字节数
#include <stdio.h> |

头文件: stdlib.h
realloc后,申请空间比原来大,重新分配地址空间
#include <stdio.h> |


string.h
int column[MAX_N];
memset(column, 0, sizeof(int) * MAX_N);
ax为0时,输出15
ax不为0时,输出6
#include <stdio.h> |
线段树详解「汇总级别整理 🔥🔥🔥」 - 我的日程安排表 I - 力扣(LeetCode)
(6条消息) 线段树详解 (原理,实现与应用)_岩之痕的博客-CSDN博客_线段树
线段树用于解决区间和问题,且该区间会被修改。
如果需要多次求某区间的和,可以使用前缀和。如果对某个元素进行修改,或者对某个区间内的元素进行修改,则前缀和不再适用。线段树每个节点代表一个区间,节点的值是区间的和。对于数组$nums=[1,2,3,4,5]$:
每个节点不仅可以用于表示区间的和
数字之和「总数字之和 = 左区间数字之和 + 右区间数字之和」
最大公因数 (GCD)「总 GCD = gcd(左区间 GCD, 右区间 GCD)」
最大值「总最大值 = max(左区间最大值,右区间最大值)」
不符合区间加法的例子:
众数「只知道左右区间的众数,没法求总区间的众数」
01 序列的最长连续零「只知道左右区间的最长连续零,没法知道总的最长连续零」
(50条消息) 线段树 4n 开四倍空间的原因_Andy-Miao的博客-CSDN博客
可以使用数组表示一颗线段树:
假设根节点为i,左孩子为2*i,右孩子为2*i+1(数组下标从1开始)
假设根节点为i,左孩子为2*i+1,右孩子为2*i+2(数组下标从0开始)。
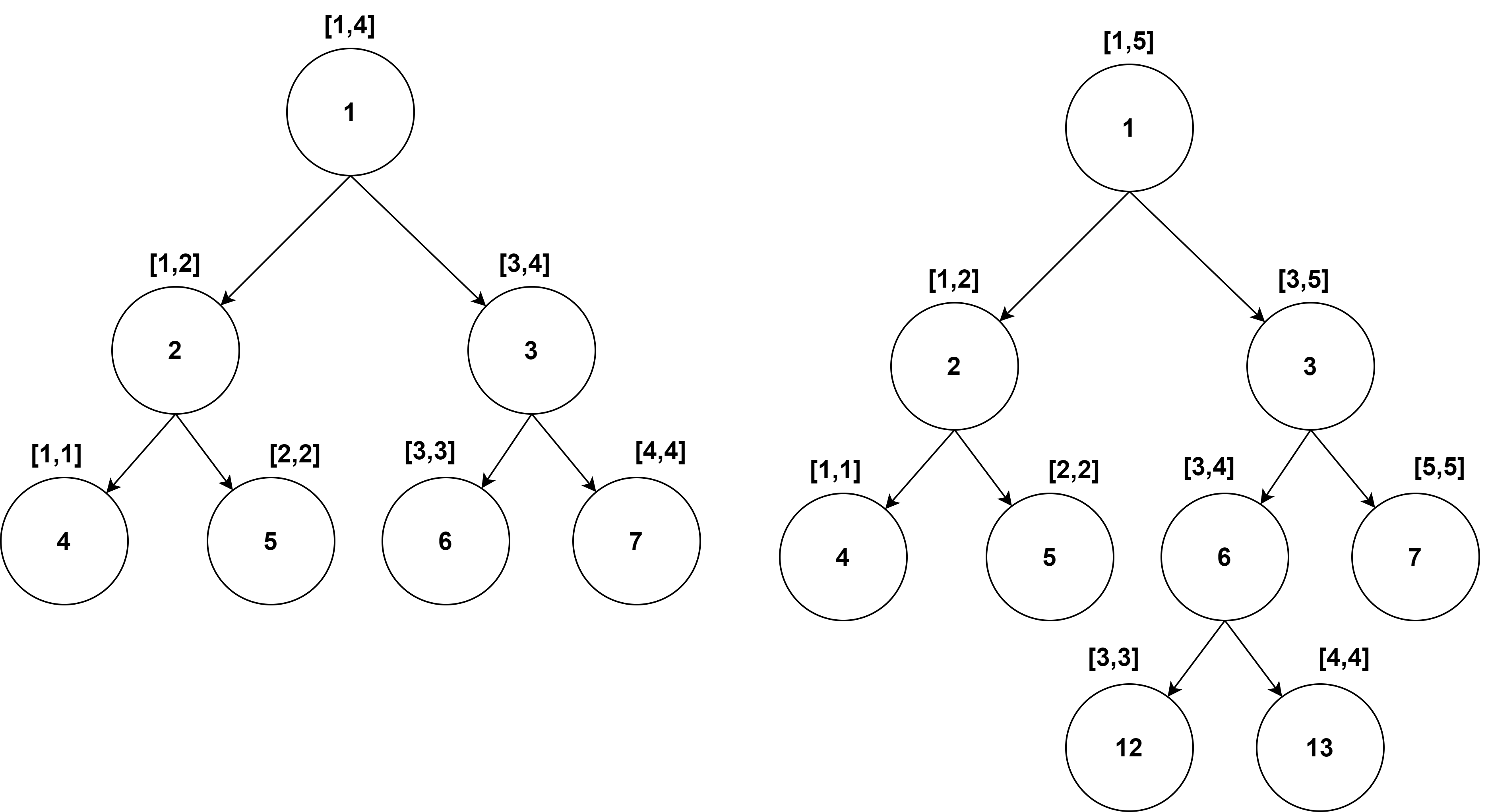
区间大小为$n=2k$,需要节点数$1+2+22+…+2k=2n-1$;$n=2{k+1}$时,需要节点$4n-1$。
当$2^k < n<2^{k+1}$时,节点落在下标[2n,4n-1)内,
链表表示线段树:
struct Node{ |
给定具体区间范围,根据范围建立线段树,此时可以用数组或者链表表示线段树。307. 区域和检索 - 数组可修改
n=nums.size(); |
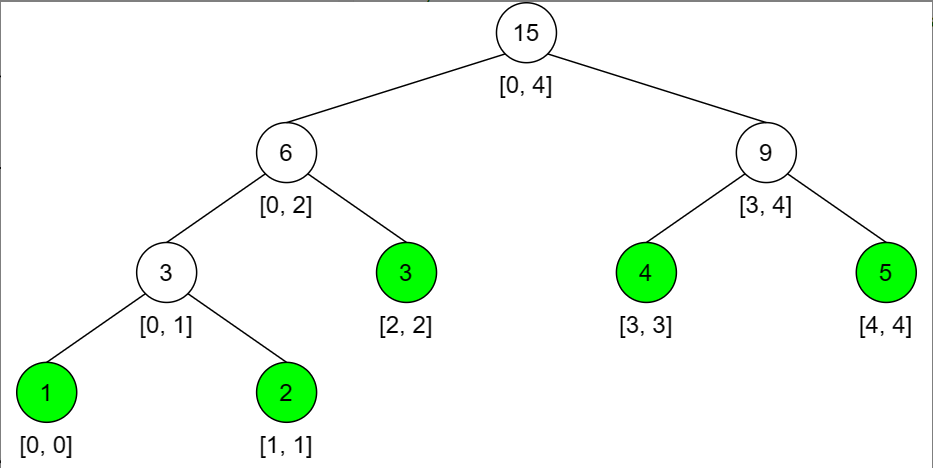
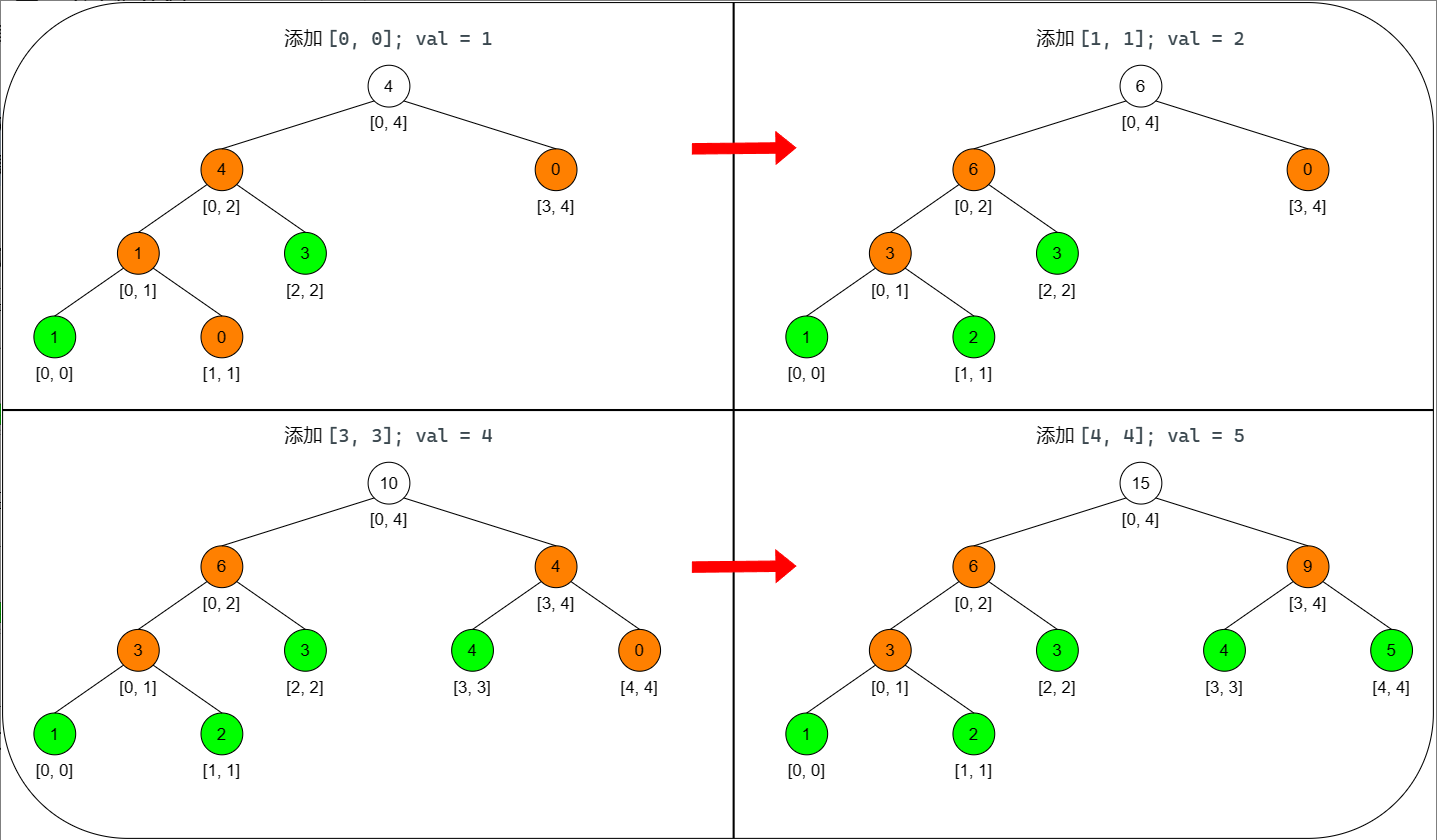
如果题目没有具体范围,只有数据的取值范围,可以采用**[动态开点线段树]**。假设数组长度为5,添加元素[2,2], val=3,update(root,0,4,2,2,3)。如果一个节点没有左右孩子,会一下子把左右孩子节点都给创建出来,如下图橙色节点所示。两个橙色的叶子节点仅仅只是被创建出来了,并无实际的值,均为 0;而另外一个橙色的非叶子节点,值为 3 的原因是下面的孩子节点的值向上更新得到的

添加节点变化,「动态开点」一般是在「更新」或「查询」的时候动态的建立节点:
更新区间[2,4]值+1,`update(root,0,4,2,4,1)。此时9号节点代表区间[3,4]都需要+1,则节点值+(end-start+1)*val,对节点添加懒惰标记lazy。当查询区间[3,3]时,懒惰标记在9号节点上,需要将标记下推给4和5号节点,同时取消标记。
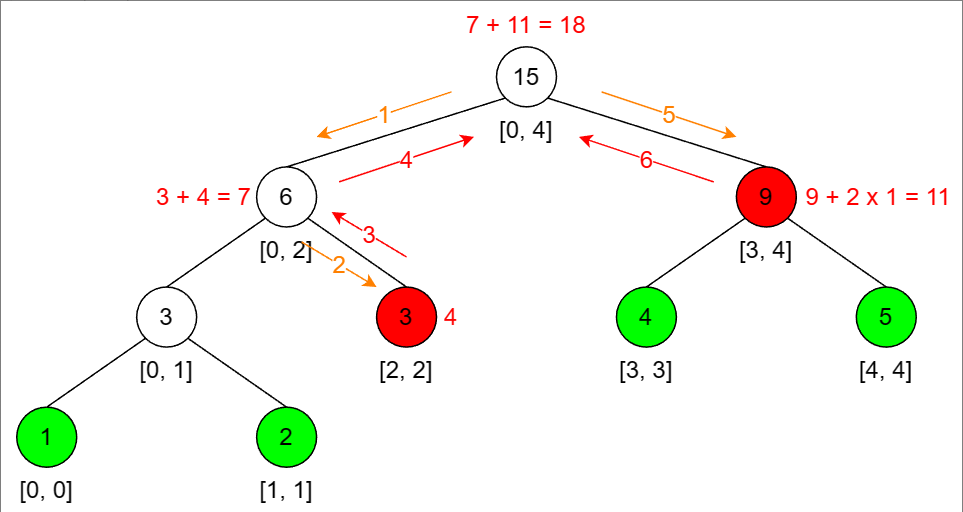
// 查询区间[l,r]区间+val |
//在当前区间[start,end],查询区间[l,r] |
class SegmentTreeDynamic { |
class MyCalendarTwo { |
class Solution { |
对于表示为「区间和」且对区间进行「加减」的更新操作的情况,我们在更新节点值的时候『需要✖️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』;我们在下推懒惰标记的时候『需要累加』!!(这种情况和模版一致!!) 如题目 最近的请求次数
对于表示为「区间和」且对区间进行「覆盖」的更新操作的情况,我们在更新节点值的时候『需要✖️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』;我们在下推懒惰标记的时候『不需要累加』!!(因为是覆盖操作!!) 如题目 区域和检索 - 数组可修改
对于表示为「区间最值」且对区间进行「加减」的更新操作的情况,我们在更新节点值的时候『不需要✖️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』;我们在下推懒惰标记的时候『需要累加』!! 如题目 我的日程安排表 I、我的日程安排表 III
class NumArray { |
class NumArray { |
class MyCalendar { |
线段树超时,但是对于track表示范围是否覆盖,lazy定义当前区间操作很有启发意义
class RangeModule { |
729. 我的日程安排表 I(区间更新,动态开点,维护区间和)
731. 我的日程安排表 II(区间更新,动态开点,维护最大值)
732. 我的日程安排表 III(区间更新,动态开点,维护最大值)
单点修改
区间查询
线段树入门【力扣双周赛 79】LeetCode_哔哩哔哩_bilibili
数组实现线段树
class BookMyShow { |
线段树区间合并法解决多次询问的「区间最长连续上升序列问题」和「区间最大子段和问题」
适用于大规模查询情况
class Solution { |
动态开点线段树
结构体中需要初始化指针为空,前面为什么不需要?代码哪里写的存在问题
class Solution { |
安装MinGW-W64提示cannot download repository.txt-解决方法s
MinGW-w64 离线包安装方法(经测试可用)
行注释 toggle line comment
块注释 toggle block comment
ctrl+shift+P修改default,setting
鼠标缩放

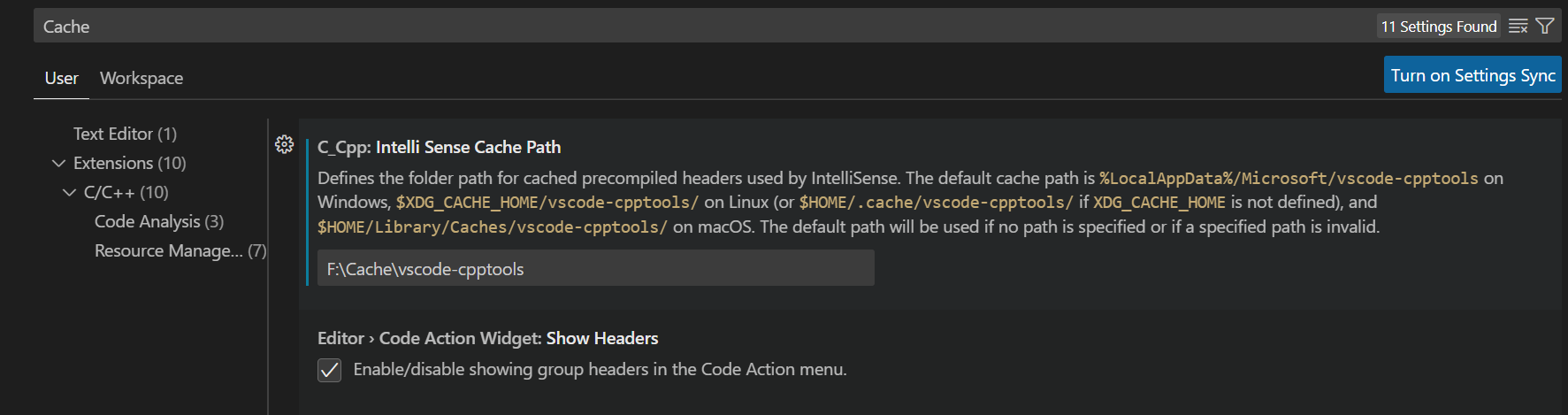
缓存大小

ipch文件夹是Intelli Sense(好像是预编译头文件之类的)这个东西产生的缓存文件